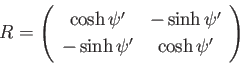1. 2次元ミンコフスキー時空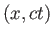 における微小世界間隔の2乗
における微小世界間隔の2乗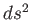 を
座標の無限小変位
を
座標の無限小変位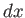 ,
,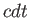 を用いて表せ。ただし
を用いて表せ。ただし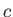 を光速とする。
を光速とする。
2. 2次元ミンコフスキー時空においてベクトル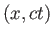 と
と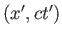 のスカラー積を求めよ。
のスカラー積を求めよ。
3. ミンコフスキー時空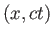 中で擬極座標
中で擬極座標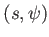
をとる。
A. このとき
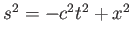 を示せ。
を示せ。
B. ベクトル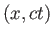 のノルムはローレンツ変換
のノルムはローレンツ変換
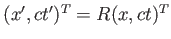
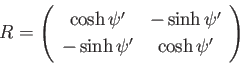 |
(3.34) |
の下で不変であることを証明せよ。
C. ベクトル
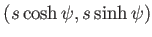 と
と
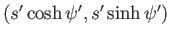 のスカラー積は
のスカラー積は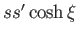 とかけることを示せ。
ただし、
とかけることを示せ。
ただし、
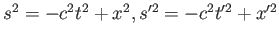 とする。
とする。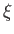 は
は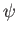 、
、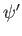 の関数とする。
の関数とする。
4. 曲率半径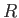 の2次元球面の計量は
の2次元球面の計量は
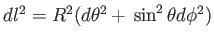 で表される。これを以下のようにして求めよう。まず、3次元ユークリッド空間に対し球座標
で表される。これを以下のようにして求めよう。まず、3次元ユークリッド空間に対し球座標
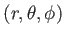 をとる。デカルト直交座標と球座標の関係は
をとる。デカルト直交座標と球座標の関係は
であるから、3次元ユークリッド空間における微小間隔の2乗
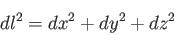 |
(3.36) |
を球座標
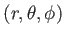 で表すと全微分
で表すと全微分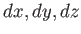 をそれぞれ
をそれぞれ
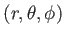 の偏微分で
表すことにより、[ ]となる。さて、
球面は
の偏微分で
表すことにより、[ ]となる。さて、
球面は 一定として求められるので、
上の式で
一定として求められるので、
上の式で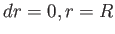 とおけばよい。
すると
とおけばよい。
すると
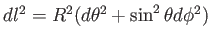 が得られる。
が得られる。
5. 4.と同様にして、曲率半径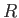 の3次元球面の計量を求めよ。
ただし、以下のような超球座標
の3次元球面の計量を求めよ。
ただし、以下のような超球座標
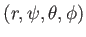 をとること。
をとること。
6. 曲率半径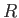 の球面の計量は
の球面の計量は
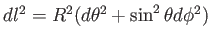 で表される。
北極点
で表される。
北極点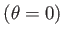 から測地的距離
から測地的距離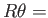 一定の点を結んで得られる円の円周の長さを
求めよ。また、その場合の円周率を
一定の点を結んで得られる円の円周の長さを
求めよ。また、その場合の円周率を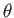 の関数として求めよ。
の関数として求めよ。
7. 曲率半径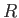 の双曲面の計量は
の双曲面の計量は
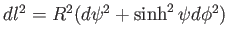 で表される。
「北極点」
で表される。
「北極点」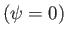 から測地的距離
から測地的距離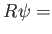 一定の点を結んで得られる円の円
周の長さを求めよ。また、その場合の円周率を
一定の点を結んで得られる円の円
周の長さを求めよ。また、その場合の円周率を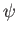 の関数として求めよ。
の関数として求めよ。
8. 赤方偏移パラメータ の天体に時計Cがおいてあるとする。
Cを地上の望遠鏡でのぞいたとき、地上で1秒進む間にCは何秒進むように観測さ
れるか?ただし、Cは宇宙膨張と共に運動しているとする。
の天体に時計Cがおいてあるとする。
Cを地上の望遠鏡でのぞいたとき、地上で1秒進む間にCは何秒進むように観測さ
れるか?ただし、Cは宇宙膨張と共に運動しているとする。