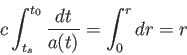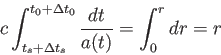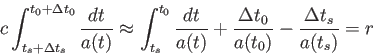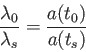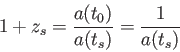FRW時空を通過する光子のエネルギーは時間と共に変化する。すなわち遠い銀河
から届いた光の波長は本来の波長より長くなる。この現象を赤方偏移とよぶ。前
章では光のドップラー効果によるものと説明したが、ハッブル距離より遠い銀河
は光以上の速さで遠ざかっているため、この説明は正しくない。赤方偏移は時空
の「曲がり」により引き起こされるのである。
時刻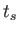 において銀河の光が原点Oにいる観測者に向かって放射されたとしよう。
また、この銀河は共動座標
において銀河の光が原点Oにいる観測者に向かって放射されたとしよう。
また、この銀河は共動座標
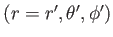 で「静止」していると仮定しよ
う。一般相対性理論によれば、光はFRW時空におけるヌル測地線に沿って進んで
くる。前節で説明した通り、角度
で「静止」していると仮定しよ
う。一般相対性理論によれば、光はFRW時空におけるヌル測地線に沿って進んで
くる。前節で説明した通り、角度
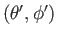 は定数となるので、ヌル測地線上
の2点間の微小世界距離は
は定数となるので、ヌル測地線上
の2点間の微小世界距離は
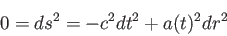 |
(3.26) |
を満たす。つまり、
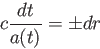 |
(3.27) |
である。左辺は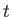 の関数で、右辺は
の関数で、右辺は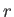 の関数であるから変数分離の形になって
いる。
の関数であるから変数分離の形になって
いる。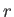 は時間と共に小さくなるが、スケール因子
は時間と共に小さくなるが、スケール因子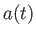 の逆数も時間と共に小さくなる
ので右辺の符号は正をとればよい。今、光波の頂である「山」が時刻
の逆数も時間と共に小さくなる
ので右辺の符号は正をとればよい。今、光波の頂である「山」が時刻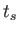 におい
て銀河を出発し、時刻
におい
て銀河を出発し、時刻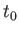 に観測者によって観測されたとしよう。すると、
式を積分することにより、
に観測者によって観測されたとしよう。すると、
式を積分することにより、
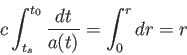 |
(3.28) |
が得られる。銀河までの共動距離は不変なのでこの積分の値は「山」が銀河を
出発した時刻に依存しないことに注意しよう。すると、次の「山」が時刻
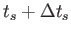 において銀河を出発し、時刻
において銀河を出発し、時刻
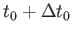 に観測者のいる原点Oに
到着したとすると、
に観測者のいる原点Oに
到着したとすると、
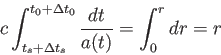 |
(3.29) |
が成立する。波長がハッブル距離より充分小さければ、式は時刻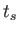 、
、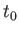 の
周りでテーラー展開することにより、
の
周りでテーラー展開することにより、
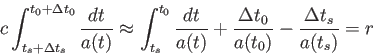 |
(3.30) |
よって、辺々引き算すると、
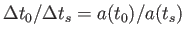 となる。「山」と「山」の時間間隔は波長
となる。「山」と「山」の時間間隔は波長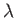 を光速
を光速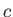 で割った量に等しい。従って、
で割った量に等しい。従って、
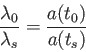 |
(3.31) |
の関係が得られる。赤方偏移パラメータ
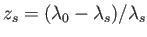 を用いると、
結局
を用いると、
結局
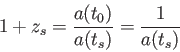 |
(3.32) |
が得られる。こうして赤方偏移パラメータ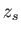 と光を発した時刻におけるスケー
ル因子
と光を発した時刻におけるスケー
ル因子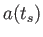 の関係が得られた。つまり、出発した時代が昔であればあるほど、
光を発した時刻一定面における宇宙の大きさが小さくなり、観測される光の波長は
より長く、光子のもつエネルギーはより小さくなるのである。
この現象を重力的赤方偏移とよぶ。
の関係が得られた。つまり、出発した時代が昔であればあるほど、
光を発した時刻一定面における宇宙の大きさが小さくなり、観測される光の波長は
より長く、光子のもつエネルギーはより小さくなるのである。
この現象を重力的赤方偏移とよぶ。