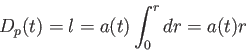空間的に一様等方な時空の空間成分は定曲率空間で表される。対応する
時空の計量はスケール因子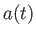 を用いて
を用いて
![\begin{displaymath}
ds^2=-c^2 dt^2+a(t)^2 [dr^2+S_\kappa (r)^2 d\Omega ^2]
\end{displaymath}](img189.png) |
(3.20) |
とかける。この計量をフリードマン-ロバートソン-ウォーカー(FRW)計量、
対応する時空をフリードマン-ロバートソン-ウォーカー(FRW) 時空とよぶ。
つまりスケール因子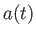 にしたがって時間と共に膨張したり収縮できる定曲率空
間を含む時空である。スケール因子
にしたがって時間と共に膨張したり収縮できる定曲率空
間を含む時空である。スケール因子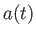 が一定でない限り、たとえ空間成分が
ゼロ曲率でもFRW時空は「曲がった」時空であることに注意しよう。なぜなら
力の働いていない質点もスケール因子
が一定でない限り、たとえ空間成分が
ゼロ曲率でもFRW時空は「曲がった」時空であることに注意しよう。なぜなら
力の働いていない質点もスケール因子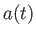 の変化に従って運動することができ
るからである。
の変化に従って運動することができ
るからである。
今空間を表す座標として極座標
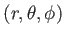 をとり、世界点
をとり、世界点
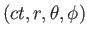 と微小距離だけ離れた別の世界点
と微小距離だけ離れた別の世界点
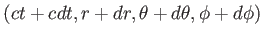 が外力の働いていない質点の
世界線上にあるとする。 世界線が原点
が外力の働いていない質点の
世界線上にあるとする。 世界線が原点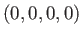 を通る場合、世界線の
空間成分は
を通る場合、世界線の
空間成分は
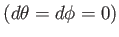 をみたす。空間の等方性から外力の働い
ていない質点は動経方向にしか運動できない。もし、質点が共動座標
で「静止」しているのであれば
をみたす。空間の等方性から外力の働い
ていない質点は動経方向にしか運動できない。もし、質点が共動座標
で「静止」しているのであれば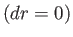 、微小世界間隔の2乗
、微小世界間隔の2乗
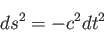 |
(3.21) |
が得られる。
しかし、相対論に不慣れな人達にとって、いつも4次元的な量を考えるのは面
倒である。出来れば3次元の量で表したい。では与えられた4次元時空に対し3次
元的な距離はどのように定義したらよいだろうか? 実はその定義の方法は無限
にある。なぜなら4次元時空から3次元を切り取る方法は無限だからである。しか
し、空間の対称性を考慮すると、空間が一様等方、すなわち定曲率空間となる
ように切り取ると都合がよい。つまり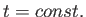 面をとればよい。その面に対し、
スケール因子
面をとればよい。その面に対し、
スケール因子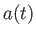 は一意に定まるので、3次元的距離は2点間の3次元的測地線の
長さに等しくなる。この距離を固有距離とよぶ。
は一意に定まるので、3次元的距離は2点間の3次元的測地線の
長さに等しくなる。この距離を固有距離とよぶ。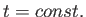 面で世界間隔は
面で世界間隔は
![\begin{displaymath}
dl^2=a(t)^2 [dr^2+S_\kappa (r)^2 d\Omega^2]
\end{displaymath}](img198.png) |
(3.22) |
とかける。観測者が共動座標
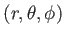 の原点
の原点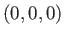 で「静止」しているとする。
このとき、共動座標
で「静止」しているとする。
このとき、共動座標
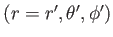 で「静止」している銀河までの固有距離
で「静止」している銀河までの固有距離
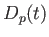 は動経方向の共動座標
は動経方向の共動座標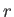 で積分することにより、
で積分することにより、
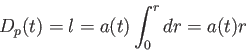 |
(3.23) |
となる。なぜなら測地線上で角度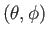 は定数だからである。固有距
離
は定数だからである。固有距
離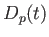 の時間微分は銀河の後退速度の大きさとみなせる。
の時間微分は銀河の後退速度の大きさとみなせる。
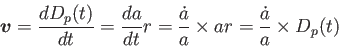 |
(3.24) |
より、
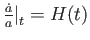 とおけば任意の時刻
とおけば任意の時刻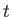 においてハッブルの法則
においてハッブルの法則
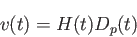 |
(3.25) |
が成立する。