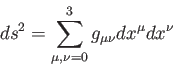空間内で近接した2点間の距離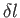 が最小になるような経路を測地線とい
う。同じ速さで進むのであれば、2点間の距離がじゅうぶん小さい場合、測地線
に沿って進めばもっとも早い時間で到着することができる。ただし、出発地と
目的地が大きく離れている場合、測地線に沿って進めば常にもっとも短時間で
到着できるとは限らない。球面の場合を考えよう。例えば北極点を出発地とし、
東京駅を目的地としよう。北極点を通る経線を通りオホーツク海に向かって南下
すればもっとも早く目的地にたどりつくことができる。しかし、地球は丸いので
逆方向、即ち北極海、グリーンランド、大西洋、ブラジル、南極大陸、オースト
ラリアを通って、東京駅に到着する経路もある。この経路は測地線に沿ってはい
るが、2点間の最小距離を与えているわけではない。
が最小になるような経路を測地線とい
う。同じ速さで進むのであれば、2点間の距離がじゅうぶん小さい場合、測地線
に沿って進めばもっとも早い時間で到着することができる。ただし、出発地と
目的地が大きく離れている場合、測地線に沿って進めば常にもっとも短時間で
到着できるとは限らない。球面の場合を考えよう。例えば北極点を出発地とし、
東京駅を目的地としよう。北極点を通る経線を通りオホーツク海に向かって南下
すればもっとも早く目的地にたどりつくことができる。しかし、地球は丸いので
逆方向、即ち北極海、グリーンランド、大西洋、ブラジル、南極大陸、オースト
ラリアを通って、東京駅に到着する経路もある。この経路は測地線に沿ってはい
るが、2点間の最小距離を与えているわけではない。
いま、測地線で囲まれた直角三角形を考えよう。半径1の球面の北極点
をNとし、子午線と赤道の交点をE、Eから東向きに赤道上を1/4周回った点をPと
する。三角形NEPは測地線で囲まれた直角三角形ではあるが内角は全て直角であ
る。つまり内角の和は270度にもなる。内角の和をユークリッド平面のときと
同じ180度に近づけるには三角形の大きさを出来るだけ小さくしなくてはなら
ない。一般に正の曲率をもつ面上では測地線で囲まれた三角形の内角の和は180
度より大きくなる。逆に負の曲率をもつ面上では三角形の内角の和は180度より
小さくなる。
さて今まで曲がった空間のことについて説明してきたが、
アインシュタインの特殊相対性理論によると、我々の住む宇宙は空間だけでなく
時間も含めた「時空」としてとらえなければならない。いま、時空の座標を
(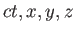 )で表すことにしよう。この座標で表される時空内の1点を世界点、
時空内の2つの事象間の「距離」を世界間隔又は世界距離とよぶ。任意の慣性系
に対し、近接した2つの事象の世界間隔の2乗はそれらの座標変化(
)で表すことにしよう。この座標で表される時空内の1点を世界点、
時空内の2つの事象間の「距離」を世界間隔又は世界距離とよぶ。任意の慣性系
に対し、近接した2つの事象の世界間隔の2乗はそれらの座標変化(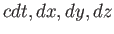 )
を用いて
)
を用いて
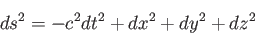 |
(3.16) |
とかける。世界間隔はローレンツ変換で不変である。外力のない質点の軌道
(世界線)はじゅうぶん近い軌道上の2点間の世界間隔の2乗を最小にすること
によって求められる。この軌道は時空の測地線と呼ばれる。重力源のない「平坦」
な時空をミンコフスキー時空とよび、その世界間隔を表す計量をミンコフスキー
計量とよぶ。重力源がある曲がった時空の世界間隔は時空の関数である
計量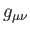 (行列
(行列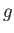 の
の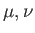 成分)を用いて
成分)を用いて
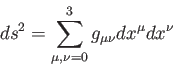 |
(3.17) |
とかける。
ここで(
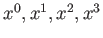 )
) (
(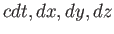 )とおいた。重力源のある
曲がった時空上でも質点の軌道は測地線に沿う。つまり曲がった時空内で
質点は「まっすぐ」に進むのである。4次元時空上で考えたときに「等速直線運
動」していても、その3次元空間成分でみると自由落下、即ち加速度運動をしている。
このときの加速度は時空の曲がり具合で決まる。
)とおいた。重力源のある
曲がった時空上でも質点の軌道は測地線に沿う。つまり曲がった時空内で
質点は「まっすぐ」に進むのである。4次元時空上で考えたときに「等速直線運
動」していても、その3次元空間成分でみると自由落下、即ち加速度運動をしている。
このときの加速度は時空の曲がり具合で決まる。
質量のない光子の運動を考えよう。光速不変の原理により、光子は経路に
沿って世界間隔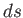 が常にゼロになるような世界線上を運動する。この世界線を
特にヌル測地線とよぶ。ミンコフスキー時空ではヌル測地線に沿って
が常にゼロになるような世界線上を運動する。この世界線を
特にヌル測地線とよぶ。ミンコフスキー時空ではヌル測地線に沿って
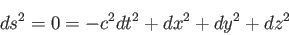 |
(3.18) |
が成立する。今空間を表す座標として極座標(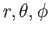 )をとり、世界点
(
)をとり、世界点
(
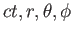 )と微小距離離れた別の世界点(
)と微小距離離れた別の世界点(
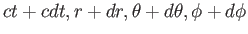 )がヌル測地線上にあるとする。 ヌル測地線
が原点(
)がヌル測地線上にあるとする。 ヌル測地線
が原点(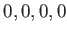 )を通る場合、測地線の空間成分は(
)を通る場合、測地線の空間成分は(
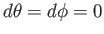 )をみたす。
つまり動経に沿って運動する。なぜなら空間成分に関してじゅうぶん近い2点の
間隔は測地線上で最小になるからである(時間成分については最大)。
従って、光子の世界線は
)をみたす。
つまり動経に沿って運動する。なぜなら空間成分に関してじゅうぶん近い2点の
間隔は測地線上で最小になるからである(時間成分については最大)。
従って、光子の世界線は
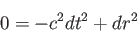 |
(3.19) |
に従う。これから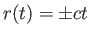 が得られる。曲がった時空内を運動する場合にも
光子はヌル測地線
が得られる。曲がった時空内を運動する場合にも
光子はヌル測地線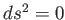 に沿って運動する。重力以外の外力の働い
ていない光子は曲がった時空内で「まっすぐ」に進むのである。
言い換えると、光子は質量が0にもかかわらず、その3次元的運動を考えると
「自由落下」しているのである。
に沿って運動する。重力以外の外力の働い
ていない光子は曲がった時空内で「まっすぐ」に進むのである。
言い換えると、光子は質量が0にもかかわらず、その3次元的運動を考えると
「自由落下」しているのである。