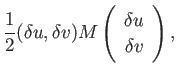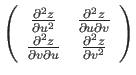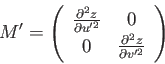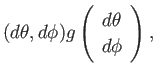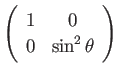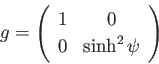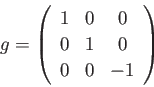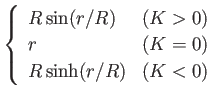曲線の曲がり具合を記述するのに便利な量の1つが曲率である。いま一定の速度
で車を運転することを考えよう。車が急カーブにさしかかると横方向に強い遠心
力を受ける。この遠心力が強ければ強いほどカーブは急である。速さが1のとき、
遠心力の大きさを質量で割った値、すなわち加速度の大きさ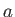 を曲線の曲率
を曲線の曲率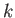 とよ
ぶ。また
とよ
ぶ。また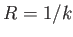 を曲率半径とよぶ。等速円運動の加速度は
を曲率半径とよぶ。等速円運動の加速度は
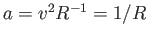 であ
るので、その場所における曲率半径が同じであれば曲線は等速円運動と同じ遠心
力をもつ。一般に曲線はさまざまな曲率半径をもつ円の包絡線としてあらわすこ
とができる。
であ
るので、その場所における曲率半径が同じであれば曲線は等速円運動と同じ遠心
力をもつ。一般に曲線はさまざまな曲率半径をもつ円の包絡線としてあらわすこ
とができる。
同様に2次元面の曲がり具合も曲率を使ってあらわすことができる。
いま曲面の高さ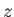 が2つのパラメータ
が2つのパラメータ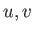 で表されているとする。この曲面
で表されているとする。この曲面
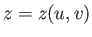 上の点Pを通る曲面上の曲線の曲率を求めるには以下のようにすればよ
い。曲率は面自体を傾けても変化しないので面が点Pで水平面に接するように傾
きを調節する。点P上でテーラー展開すると高さ
上の点Pを通る曲面上の曲線の曲率を求めるには以下のようにすればよ
い。曲率は面自体を傾けても変化しないので面が点Pで水平面に接するように傾
きを調節する。点P上でテーラー展開すると高さ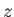 の点Pから微小ベクトル
の点Pから微小ベクトル
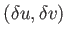 だけ離れている地点における曲面の高さ
だけ離れている地点における曲面の高さ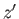 を2次形式
で近似することができる。
を2次形式
で近似することができる。
ここで行列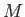 をヘッセ行列とよぶ。
をヘッセ行列とよぶ。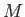 は対称行列なので直交変換すなわち
座標の回転によって対角化ができる。この回転変換で座標は
は対称行列なので直交変換すなわち
座標の回転によって対角化ができる。この回転変換で座標は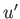 ,
,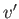 に
変換されたとする。対角化されたヘッセ行列はこの新しい座標系で
に
変換されたとする。対角化されたヘッセ行列はこの新しい座標系で
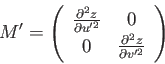 |
(3.5) |
とかける。さてヘッセ行列の行列式
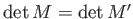 、すなわち回転変換
で不変である。この不変量をガウス曲率
、すなわち回転変換
で不変である。この不変量をガウス曲率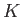 とよび、2次元面の曲がり具合を表す。
対角化されたヘッセ行列で表すと
とよび、2次元面の曲がり具合を表す。
対角化されたヘッセ行列で表すと
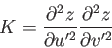 |
(3.6) |
とかける。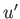 ,
,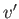 は長さを表すのでそれぞれ
は長さを表すのでそれぞれ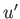 ,
,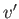 を「時間」を表すパラメーターと
考えると
を「時間」を表すパラメーターと
考えると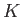 の因子はそれぞれ速さが1のときに
の因子はそれぞれ速さが1のときに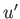 軸、もしくは
軸、もしくは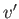 軸に沿って運動する
粒子の加速度、すなわち1次元の曲率に対応する。これらの曲率をベクトル
軸に沿って運動する
粒子の加速度、すなわち1次元の曲率に対応する。これらの曲率をベクトル
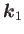 ,
,
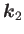 で表すとガウス曲率は内積
で表すとガウス曲率は内積
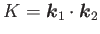 と書き表せる。値が正
のとき正曲率、負のとき負曲率とよぶ。値がゼロのときは平坦とよぶ。
曲率
と書き表せる。値が正
のとき正曲率、負のとき負曲率とよぶ。値がゼロのときは平坦とよぶ。
曲率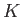 がゼロでない場合、1次元曲率
がゼロでない場合、1次元曲率
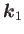 ,
,
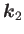 にそれぞ
れ対応する曲率半径を
にそれぞ
れ対応する曲率半径を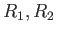 とすると
とすると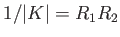 とかける。したがってガウス
曲率の次元は長さを
とかける。したがってガウス
曲率の次元は長さを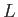 とすると[
とすると[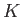 ]=[
]=[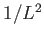 ]である。
]である。
等方で一様な2次元面はガウス曲率(以後、単に「曲率」とよぶ。)が場所によ
らず一定であり、曲率の符号によって3種類に分類される。
すなわち正の定曲率をもつ球面、負の定曲率
をもつ双曲面、曲率がゼロのユークリッド平面である。曲率がゼロでない曲がっ
た空間はユークリッド幾何学の公理をみたさない。例えば、球面上ではある直線
に平行な直線はそれ以外には一本も存在しない。一方、双曲面上ではある直線に
平行な直線は無限に存在する。これらの曲がった面に対して成り立つ幾何学を
非ユークリッド幾何学とよぶ。アインシュタインは物質やエネルギーによっ
て時空が曲がるため、時空は一般に非ユークリッド幾何学で記述されるだろうと
推論した。
面の曲がり具合を記述するのに便利な方法がもう一つある。
平坦な面、すなわち曲率ゼロのユークリッド平面上に近接した2点
があり、その距離が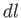 で表されるとしよう。その面上に直交座標(
で表されるとしよう。その面上に直交座標(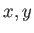 ) をとる。
ピタゴラスの定理から2点間の距離の2乗は
) をとる。
ピタゴラスの定理から2点間の距離の2乗は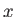 軸方向の距離の2乗と
軸方向の距離の2乗と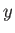 軸方向の距離
の2乗の和に等しい。すなわち
軸方向の距離
の2乗の和に等しい。すなわち
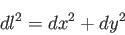 |
(3.7) |
とかける。直角三角形の斜辺の2乗は底辺の2乗と高さの2乗の和に等しい。では
曲がった面ではどうだろうか?例えば正の定曲率をもつ球面を考えよう。球の半
径が1であったとすると、球座標(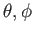 ) をとることにより、球面上の「ピタゴ
ラスの定理」は以下のようにかける。
) をとることにより、球面上の「ピタゴ
ラスの定理」は以下のようにかける。
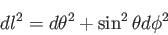 |
(3.8) |
以上の式を2次形式で表すと、
とかける。ユークリッド平面の場合と異なり、行列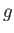 は面上の位置
座標
は面上の位置
座標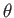 の関数となるため、ピタゴラスの定理は特別な点
(
の関数となるため、ピタゴラスの定理は特別な点
(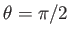 )をのぞいて成立しない。
)をのぞいて成立しない。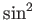 が1より
小さいため直角三角形の斜辺の長さの2乗は底辺の2乗と
高さの2乗の和より小さくなってしまう。
このピタゴラスの定理からのずれをあらわす行列
が1より
小さいため直角三角形の斜辺の長さの2乗は底辺の2乗と
高さの2乗の和より小さくなってしまう。
このピタゴラスの定理からのずれをあらわす行列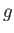 を計量(もしくは
計量テンソル)とよぶ。負の定曲率の面の場合、計量は以下のように
表される。
を計量(もしくは
計量テンソル)とよぶ。負の定曲率の面の場合、計量は以下のように
表される。
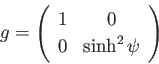 |
(3.10) |
負の定曲率の面の面積は無限だが、3次元ユークリッド空間に埋め込む
ことはできない。馬の鞍やトランペットの表面は負の曲率をもつが
その形をつなげて面を閉じさせることはできない。そのかわり、
3次元ミンコフスキー空間すなわち計量が座標(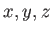 )に対し
)に対し
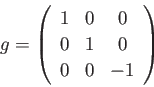 |
(3.11) |
で表せる空間に埋め込むことが出来る。その場合、負の定曲率面は双曲線
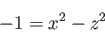 |
(3.12) |
を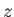 軸の周りに回転させてできる2つの双曲面の片方(どちらでもよい)
として表される。
軸の周りに回転させてできる2つの双曲面の片方(どちらでもよい)
として表される。
曲率と計量はどのように関係しているのだろうか?正の定曲率をもつ半径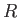 の球面を考えよう。半径1の場合と座標が同じであっても、球面上の2点間
の距離は
の球面を考えよう。半径1の場合と座標が同じであっても、球面上の2点間
の距離は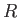 倍になる。したがって近接した2点間の座標変化を(
倍になる。したがって近接した2点間の座標変化を(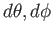 )とすると
2点間の距離の2乗は
)とすると
2点間の距離の2乗は
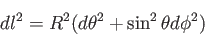 |
(3.13) |
とかける。面上のどの場所においても曲率半径は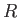 に等しいので
ガウス曲率は
に等しいので
ガウス曲率は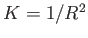 となる。
となる。
負の定曲率の場合も同様である。近接した2点間の座標間隔を(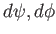 )
とすると、2点間の距離の2乗は
)
とすると、2点間の距離の2乗は
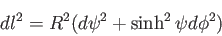 |
(3.14) |
となる。このとき双曲面の曲率半径は面上のどの場所においても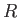 に等しく
なる。また、ガウス曲率は
に等しく
なる。また、ガウス曲率は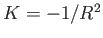 となる。
となる。
ガウス曲率を3次元以上の次元をもつ空間に対して一般化するには
どうしたらよいだろうか?そのためには空間から2次元部分を任意に
切り出して、その面に対してガウス曲率を求めればよい。このとき決まる
ガウス曲率を断面曲率という。断面曲率が面の切り出し方によらず一定の場合、
定曲率空間とよぶ。3次元の定曲率空間は、曲率ゼロ、正、負の3種類があり、
計量はそれぞれ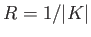 を用いて、
を用いて、
となる。定曲率空間は一様等方であり、その逆も成立する。