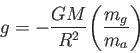物体の質量を測るには2つの方法がある。1つ目は物体にかかる重力を用いる方
法である。2つの球体の質量をそれぞれ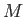 ,
,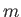 とする。中心間の距離を
とする。中心間の距離を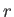 と
すると2つの球体にはたらく重力は万有引力の法則により、引力の向く方向を負
と定義すれば
と
すると2つの球体にはたらく重力は万有引力の法則により、引力の向く方向を負
と定義すれば
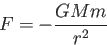 |
(3.1) |
と表される。この重力を用いて測定される質量を重力質量とよぶ。2つ目の方法
は、物体にはたらく加速度を用いるものである。ニュートンの第2法則によると
力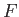 と加速度
と加速度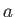 の間には
の間には
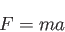 |
(3.2) |
の関係がある。重力はゼロでも加速度を用いれば質量を測ることができる。
こうして測定される質量を慣性質量とよぶ。この2つの方法で測定された質量が
同じである、即ち重力質量と慣性質量が同一であることを等価原理とよぶ。も
し、等価原理が成立しないとどうなるのであろうか?地球の表面近くにある小物
体の重力加速度を考えてみよう。地球の質量を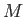 、地球の半径を
、地球の半径を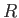 、鉛直下向きを
負とすると重力加速度
、鉛直下向きを
負とすると重力加速度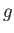 は小物体の重力質量
は小物体の重力質量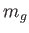 慣性質量
慣性質量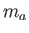 を用いて
を用いて
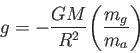 |
(3.3) |
とかける。もし、等価原理が成立していないのであれば、比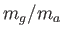 が物体や
組成ごとに異なり、重力加速度も一定ではないことになる。しかし、実験による
と重力加速度は極めて良い精度で一定値をとり、重力質量と慣性質量
は
が物体や
組成ごとに異なり、重力加速度も一定ではないことになる。しかし、実験による
と重力加速度は極めて良い精度で一定値をとり、重力質量と慣性質量
は
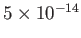 以内で等しいことが分かっている。つまり重力質量と慣性質
量は事実上「等しい」のである。
以内で等しいことが分かっている。つまり重力質量と慣性質
量は事実上「等しい」のである。
アインシュタインは等価原理に基づいて重力場中では時空が「ゆがむ」ことを
次の思考実験により導き出した。いま宇宙船が地上で静止していたとする。この
とき宇宙船の物体には鉛直下向きに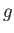 の大きさをもつ重力加速度がかかって
いる。さてこの宇宙船が地球を離れ、天体の重力の影響を受けない宇宙空間に
出たとする。このとき宇宙船が進行方向に一定の加速度
の大きさをもつ重力加速度がかかって
いる。さてこの宇宙船が地球を離れ、天体の重力の影響を受けない宇宙空間に
出たとする。このとき宇宙船が進行方向に一定の加速度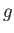 で運動すれば、
船内の物体には大きさ
で運動すれば、
船内の物体には大きさ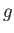 のみかけの力、すなわち慣性力が逆向きに働く
であろう。このとき、宇宙船内にいる人は地上にいるのか宇宙空間にいるのか
区別することができるであろうか?アインシュタインはこの問に否と答えた。
宇宙船の大きさが地球に比べじゅうぶん小さい限り、区別することはできないの
である。なぜなら重力質量と慣性質量は等しいからである。さて、一定の加速度
で運動している宇宙船内で加速の向きに垂直に光を飛ばしてみよう。重力のない
場所で光はまっすぐに進むはずであるから、宇宙船内では光線の経路は曲がる
であろう。もし、宇宙船内にいる人が地上にいるのか宇宙空間にいるのか区別
することができないのであれば、地上で静止している宇宙船内でも同じ現象が
起こるだろう。つまり、光線の経路は同様に曲がるであろう。アインシュタイン
はこの重力場中での光線の曲がりを「時空のゆがみ」で説明することに成功した。
光はゆがんだ時空中をまっすぐに進む。この経路を光の測地線とよぶ。重力のな
い場所で加速運動する系では時空はゆがまない。そのかわりに座標がゆがむ。重
力のある場所で静止している系では座標はゆがまない。そのかわり時空がゆがむ。
両者は時空の大きなスケールでは異なる現象であるが、小スケールで比較すると
違いがない。時空のゆがみを正確に記述するには微分幾何学とよばれる数学
を使う必要があるが、次節でくわしく述べることにする。
のみかけの力、すなわち慣性力が逆向きに働く
であろう。このとき、宇宙船内にいる人は地上にいるのか宇宙空間にいるのか
区別することができるであろうか?アインシュタインはこの問に否と答えた。
宇宙船の大きさが地球に比べじゅうぶん小さい限り、区別することはできないの
である。なぜなら重力質量と慣性質量は等しいからである。さて、一定の加速度
で運動している宇宙船内で加速の向きに垂直に光を飛ばしてみよう。重力のない
場所で光はまっすぐに進むはずであるから、宇宙船内では光線の経路は曲がる
であろう。もし、宇宙船内にいる人が地上にいるのか宇宙空間にいるのか区別
することができないのであれば、地上で静止している宇宙船内でも同じ現象が
起こるだろう。つまり、光線の経路は同様に曲がるであろう。アインシュタイン
はこの重力場中での光線の曲がりを「時空のゆがみ」で説明することに成功した。
光はゆがんだ時空中をまっすぐに進む。この経路を光の測地線とよぶ。重力のな
い場所で加速運動する系では時空はゆがまない。そのかわりに座標がゆがむ。重
力のある場所で静止している系では座標はゆがまない。そのかわり時空がゆがむ。
両者は時空の大きなスケールでは異なる現象であるが、小スケールで比較すると
違いがない。時空のゆがみを正確に記述するには微分幾何学とよばれる数学
を使う必要があるが、次節でくわしく述べることにする。