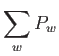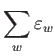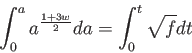宇宙の膨張を論じる際に重要な性質は、考えている成分の状態方程式である。
物質の組成や大きさ、種類、それぞれの場所における密度などは宇宙スケールで
平均化してしまうと、宇宙膨張に対してはほとんど影響を及ぼさない。つまり、
水素だろうがヘリウムだろうが、その状態方程式以外の物理量は考えなくてもよいのである。
宇宙の成分は大きく分けて3種類ある。第一の成分は状態方程式パラメータ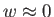 の非相対論的粒子である。これはバリオンとよばれる比較的質量の大きい粒子
(中性子や陽子)やレプトンとよばれる比較的質量の小さい粒子(電子など)、
そして正体不明のダークマター粒子などに対応する。ただし、宇宙初期において
充分温度が高くなると、これらの粒子も相対論的粒子としてふるまうことに注意
する必要がある。以降は簡単のため「物質」成分とよぶことにする。第二の成分
は状態方程式パラメータ
の非相対論的粒子である。これはバリオンとよばれる比較的質量の大きい粒子
(中性子や陽子)やレプトンとよばれる比較的質量の小さい粒子(電子など)、
そして正体不明のダークマター粒子などに対応する。ただし、宇宙初期において
充分温度が高くなると、これらの粒子も相対論的粒子としてふるまうことに注意
する必要がある。以降は簡単のため「物質」成分とよぶことにする。第二の成分
は状態方程式パラメータ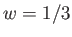 の相対論的粒子、すなわち光子やニュートリノで
ある。ただし、ニュートリノはわずかに質量を持っているため、現在は非相対論
的成分になっている可能性があることに注意しなければならない。以降は簡単の
ため「輻射」成分とよぶことにする。第三の成分はダークエネルギーである。そ
の有力な候補として考えられているのは状態方程式パラメータ
の相対論的粒子、すなわち光子やニュートリノで
ある。ただし、ニュートリノはわずかに質量を持っているため、現在は非相対論
的成分になっている可能性があることに注意しなければならない。以降は簡単の
ため「輻射」成分とよぶことにする。第三の成分はダークエネルギーである。そ
の有力な候補として考えられているのは状態方程式パラメータ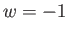 の宇宙定数
の宇宙定数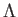 であるが正確に定数なのか未だ不明である。これらの3成分の相対的な量は宇宙
の年齢と共に変化することに注意しよう。例えば、宇宙スケールで平均化した
物質の平均密度はスケール因子
であるが正確に定数なのか未だ不明である。これらの3成分の相対的な量は宇宙
の年齢と共に変化することに注意しよう。例えば、宇宙スケールで平均化した
物質の平均密度はスケール因子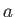 の3乗に反比例する。しかし、輻射成分である
相対論的粒子の平均エネルギー密度はスケール因子
の3乗に反比例する。しかし、輻射成分である
相対論的粒子の平均エネルギー密度はスケール因子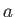 の
4乗に反比例する。これは輻射の波長がスケール因子
の
4乗に反比例する。これは輻射の波長がスケール因子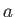 に比例して大きくなるため、
1粒子あたりのエネルギーがスケール因子
に比例して大きくなるため、
1粒子あたりのエネルギーがスケール因子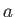 に反比例するからである。このことは流体方程式
に反比例するからである。このことは流体方程式
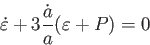 |
(5.1) |
を使って次のように示すことができる。宇宙が1成分から成るモデルを考えよう。
この成分の状態方程式パラメータを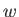 とする。仮定より、
とする。仮定より、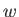 は時間や場所によ
らず一定である。この成分のエネルギー密度を
は時間や場所によ
らず一定である。この成分のエネルギー密度を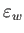 としよう。
すると流体方程式は
としよう。
すると流体方程式は
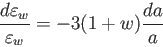 |
(5.2) |
と変数分離できる。両辺を積分すると
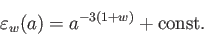 |
(5.3) |
が得られる。現在スケール因子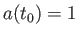 であるから、現在のエネルギー密度
を
であるから、現在のエネルギー密度
を
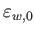 とおくと
とおくと
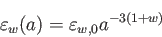 |
(5.4) |
となる。つまり、エネルギー密度をスケール因子の関数として書き表すことがで
きる。輻射成分に対しては、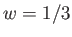 であるから、輻射のエネルギー密度は
であるから、輻射のエネルギー密度は
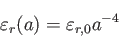 |
(5.5) |
となる。つまり相対論的粒子からなる流体のエネルギー密度はスケール因子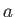 の4
乗に反比例する。
の4
乗に反比例する。
さて、宇宙が多成分から成る場合もこの結果が成立するのだろうか?
お互いが因果関係をもたない充分大きなスケールで宇宙を平均すると、異なる成
分同士の相互作用(輻射と物質の間など)は無視できることに注意しよう。この
とき、ある時刻における宇宙の全平均エネルギー密度と全平均圧力は個々の成分の和
として書き表せる。異なる成分の間でエネルギーのやりとりが無視出来るのであ
れば、各成分に対してエネルギー保存則が成立しているはずである。つまり、
流体方程式はどの成分についても成立しなければならず、宇宙が多成分から成
る場合も
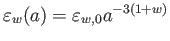 は成立するので
ある。結局、輻射成分はスケール因子
は成立するので
ある。結局、輻射成分はスケール因子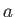 の4乗に反比例し、速度の小さい物質成
分はスケール因子
の4乗に反比例し、速度の小さい物質成
分はスケール因子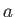 の3乗に反比例し、宇宙定数
の3乗に反比例し、宇宙定数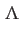 はスケール因子によらず一
定であることが分かる。このことから、エネルギー密度への寄与という点におい
ては、宇宙初期では輻射成分が優勢であり、その後宇宙がある程度膨張すると
物質成分、そしてさらに膨張すると宇宙定数が優勢になる。つまり、宇宙の年齢
と共に、各成分の割合が変化するのである。
はスケール因子によらず一
定であることが分かる。このことから、エネルギー密度への寄与という点におい
ては、宇宙初期では輻射成分が優勢であり、その後宇宙がある程度膨張すると
物質成分、そしてさらに膨張すると宇宙定数が優勢になる。つまり、宇宙の年齢
と共に、各成分の割合が変化するのである。
次に、宇宙空間が平坦で、物質(エネルギー)の状態方程式パラメータが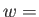 一定である
1成分宇宙を調べてみよう。このときのエネルギー密度を
一定である
1成分宇宙を調べてみよう。このときのエネルギー密度を
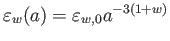 とおくと、フリードマン方程式
とおくと、フリードマン方程式
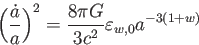 |
(5.7) |
は次のように変数分離することができる。
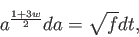 |
(5.8) |
ここで
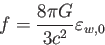 |
(5.9) |
である。
両辺を積分すると、
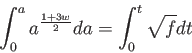 |
(5.10) |
から、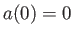 より、
より、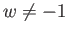 に対して
に対して
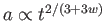 が、
が、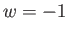 に対しては、
に対しては、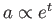 が得られる。この結果から以下のことがいえる。まず輻射成分が
優勢な時代を考えよう。このとき、宇宙は輻射のみをもつ1成分
宇宙モデルで記述することができる。
が得られる。この結果から以下のことがいえる。まず輻射成分が
優勢な時代を考えよう。このとき、宇宙は輻射のみをもつ1成分
宇宙モデルで記述することができる。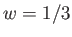 であるので
であるので
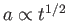 である。
スケール因子
である。
スケール因子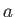 の2階微分
の2階微分
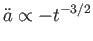 は負であるので減速膨張
である。次に物質成分が優勢な時代を考えよう。このとき、宇宙は物質
のみをもつ1成分宇宙モデルで記述することができる。
は負であるので減速膨張
である。次に物質成分が優勢な時代を考えよう。このとき、宇宙は物質
のみをもつ1成分宇宙モデルで記述することができる。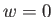 であるので
であるので
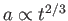 である。スケール因子
である。スケール因子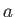 の2階微分
の2階微分
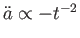 は負であるので減速膨張である。最後に宇宙定数
は負であるので減速膨張である。最後に宇宙定数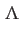 が優勢な時代を考え
よう。このとき、宇宙は宇宙定数
が優勢な時代を考え
よう。このとき、宇宙は宇宙定数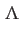 のみをもつ1成分宇宙モデルで記述
することができる。
のみをもつ1成分宇宙モデルで記述
することができる。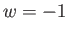 であるので
であるので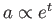 である。したがって、
スケール因子
である。したがって、
スケール因子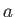 の2階微分
の2階微分
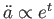 は正であるので加速膨張である。
は正であるので加速膨張である。