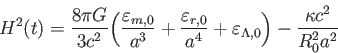次に、より現実的な多成分から成る宇宙モデルを考えよう。ここでは3種類の一様な成分、即ち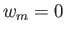 の質量(非相対論的粒子)、
の質量(非相対論的粒子)、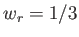 の輻射(相対論的粒子)、
の輻射(相対論的粒子)、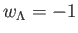 の宇宙定数(
の宇宙定数(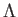 )を含むFRWモデルを考える。この場合、宇宙の過去、現
在、未来の姿はどのようなものになるであろうか?
まず、これらの宇宙の成分は全て独立であると仮定する。また各成分の状態方程式パラ
メータ
)を含むFRWモデルを考える。この場合、宇宙の過去、現
在、未来の姿はどのようなものになるであろうか?
まず、これらの宇宙の成分は全て独立であると仮定する。また各成分の状態方程式パラ
メータ
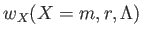 は時間的に不変とする。すると、宇宙膨張を表すスケール因子
は時間的に不変とする。すると、宇宙膨張を表すスケール因子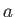 と各成分のエネルギー密度
と各成分のエネルギー密度
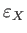 の時間発展
の時間発展
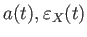 は以下の方程式を解くことによって求めることができる。
は以下の方程式を解くことによって求めることができる。
この内、流体方程式は各成分に対して独立であるので、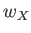 がそれぞれ
定数であれば、1成分宇宙の場合と同様に
がそれぞれ
定数であれば、1成分宇宙の場合と同様に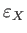 を
を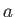 の関数として
解くことができる。
の関数として
解くことができる。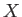 成分の現在におけるエネルギー密度
成分の現在におけるエネルギー密度
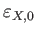 を用いると
を用いると
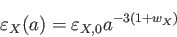 |
(5.14) |
とかける。つまり、現在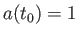 におけるエネルギー密度が分かれば、過去や未来の
エネルギー密度も計算することができるのである。
これらの解をフリードマン方程式に代入して微分方程式を解き、現在の曲率半径
におけるエネルギー密度が分かれば、過去や未来の
エネルギー密度も計算することができるのである。
これらの解をフリードマン方程式に代入して微分方程式を解き、現在の曲率半径
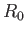 、エネルギー密度
、エネルギー密度
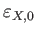 、宇宙の膨張率を表す
ハッブル定数
、宇宙の膨張率を表す
ハッブル定数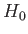 を与えればスケール因子の時間発展
を与えればスケール因子の時間発展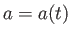 が求まる。
が求まる。
さて、宇宙初期を除くと、エネルギー密度は非常に小さい値であるので、無次元の
密度パラメータを用いると分かりやすい。時刻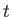 における各成分の密度パラメー
タは
における各成分の密度パラメー
タは
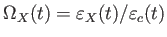 である。計算に必要なのは
ある時刻における各成分の密度パラメータの値であるが、
ここでは現在
である。計算に必要なのは
ある時刻における各成分の密度パラメータの値であるが、
ここでは現在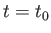 における値
における値
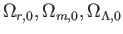 を考える。さらに
ハッブル定数
を考える。さらに
ハッブル定数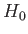 が分かれば、宇宙膨張を表すスケール因子の時間発展
が分かれば、宇宙膨張を表すスケール因子の時間発展
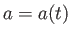 を完全に決定することができる。これらの密度パラメータを用いてフリードマン方程式を無次元化してみよう。時刻
を完全に決定することができる。これらの密度パラメータを用いてフリードマン方程式を無次元化してみよう。時刻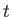 におけるフリードマン方程式は
におけるフリードマン方程式は
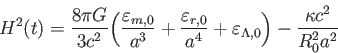 |
(5.15) |
とかける。これを現在におけるフリードマン方程式
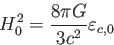 |
(5.16) |
で辺々割ると、無次元フリードマン方程式
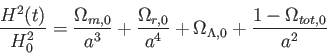 |
(5.17) |
を得る。ここで
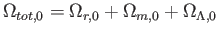 は現在の密度パラメータの総和を表す。
式(5.17)の左辺が
は現在の密度パラメータの総和を表す。
式(5.17)の左辺が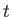 、右辺が
、右辺が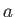 の関数になるように変数分離すると
次のような積分が得られる。
の関数になるように変数分離すると
次のような積分が得られる。
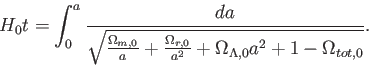 |
(5.18) |
つまり、右辺を積分することにより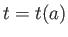 が求まる。逆変換すれば
が求まる。逆変換すれば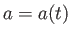 が求まる。
一般の場合、式(5.18)の右辺の積分を初等的な関数で陽に表すことは出来ず、
数値的に求める必要がある。しかし、2成分の場合は解が比較的簡単に表せる場
合がある。以下、2成分モデルにおける宇宙の膨張の様子を調べていくことにする。
が求まる。
一般の場合、式(5.18)の右辺の積分を初等的な関数で陽に表すことは出来ず、
数値的に求める必要がある。しかし、2成分の場合は解が比較的簡単に表せる場
合がある。以下、2成分モデルにおける宇宙の膨張の様子を調べていくことにする。
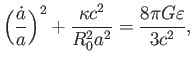
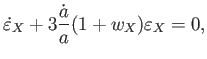
![]() における各成分の密度パラメー
タは
における各成分の密度パラメー
タは
![]() である。計算に必要なのは
ある時刻における各成分の密度パラメータの値であるが、
ここでは現在
である。計算に必要なのは
ある時刻における各成分の密度パラメータの値であるが、
ここでは現在![]() における値
における値
![]() を考える。さらに
ハッブル定数
を考える。さらに
ハッブル定数![]() が分かれば、宇宙膨張を表すスケール因子の時間発展
が分かれば、宇宙膨張を表すスケール因子の時間発展
![]() を完全に決定することができる。これらの密度パラメータを用いてフリードマン方程式を無次元化してみよう。時刻
を完全に決定することができる。これらの密度パラメータを用いてフリードマン方程式を無次元化してみよう。時刻![]() におけるフリードマン方程式は
におけるフリードマン方程式は