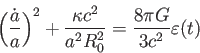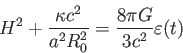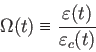質量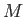 で圧力の無視出来る質量密度
で圧力の無視出来る質量密度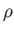 が
空間的に一定の一様球を考えよう。この球の半径
が
空間的に一定の一様球を考えよう。この球の半径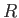 の
時間変化を求める方程式は以下のようにして求められる。球対称の場合、
球の中の質点に働く重力はその質点と球の中心を結ぶ半径内の質量だけで
決まることに注意しよう。時刻
の
時間変化を求める方程式は以下のようにして求められる。球対称の場合、
球の中の質点に働く重力はその質点と球の中心を結ぶ半径内の質量だけで
決まることに注意しよう。時刻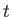 において球の中心から
において球の中心から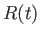 離れた場所
にある質量
離れた場所
にある質量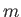 の質点に働く動径方向の引力は、万有引力定数を
の質点に働く動径方向の引力は、万有引力定数を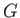 とすると、
とすると、
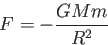 |
(4.1) |
とかける。運動方程式
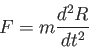 |
(4.2) |
より、方程式
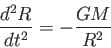 |
(4.3) |
が得られる。ここで速度の動径成分を
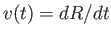 とおくと、
とおくと、
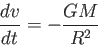 |
(4.4) |
両辺に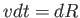 をかけて積分すると、
をかけて積分すると、
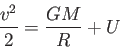 |
(4.5) |
が得られる。ここで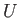 は積分定数である。さらに質量
は積分定数である。さらに質量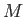 の代わりに質量密度
の代わりに質量密度
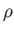 、半径
、半径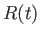 の代わりにスケール因子
の代わりにスケール因子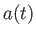 と共動距離
と共動距離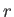 を用いて書き換えてみ
よう。すると、
を用いて書き換えてみ
よう。すると、
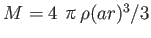 、
、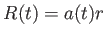 から
から
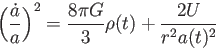 |
(4.6) |
が得られる。この式をニュートン近似におけるフリードマン方程式とよぶ。
積分定数はニュートンの理論から求めることはできないが、アインシュタインの
一般相対論を使えば、エネルギー密度
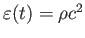 と
ガウス曲率
と
ガウス曲率 を用いて、
を用いて、
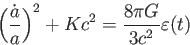 |
(4.7) |
とかける。これがフリードマン方程式である。フリードマン方程式の左辺は
宇宙の膨張率と曲率の効果、右辺は宇宙のエネルギー密度を表す。
フリードマン方程式は宇宙論におけるもっとも重要な方程式である。
さて、ガウス曲率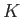 は現在の曲率半径
は現在の曲率半径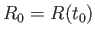 を用いて、
を用いて、
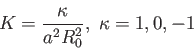 |
(4.8) |
とかける。ここで、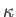 は曲率の符号である。するとフリードマン方程式は
は曲率の符号である。するとフリードマン方程式は
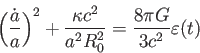 |
(4.9) |
とかける。さらにハッブルパラメータ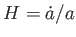 を用いると、
を用いると、
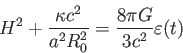 |
(4.10) |
ともかける。与えられた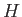 に対し、曲率がちょうどゼロになるような
エネルギー密度を臨界エネルギー密度、また対応する
質量密度を臨界質量密度と呼ぶ(まとめて臨界密度とも呼ぶ)。
臨界エネルギー密度の値は
に対し、曲率がちょうどゼロになるような
エネルギー密度を臨界エネルギー密度、また対応する
質量密度を臨界質量密度と呼ぶ(まとめて臨界密度とも呼ぶ)。
臨界エネルギー密度の値は
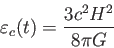 |
(4.11) |
と表され、時間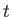 の関数である。時間
の関数である。時間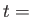 一定の面上でじゅうぶん大きい空間的
スケールで平均したエネルギー密度の値がこの値よりも大きければ、
宇宙のガウス曲率は正であり、小さければ負である。現在のハッブルパラメータ、
即ちハッブル定数
一定の面上でじゅうぶん大きい空間的
スケールで平均したエネルギー密度の値がこの値よりも大きければ、
宇宙のガウス曲率は正であり、小さければ負である。現在のハッブルパラメータ、
即ちハッブル定数
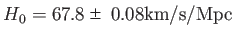 を代入すると(2013年時点の観測値)、現在における臨界エネルギー密度
は
を代入すると(2013年時点の観測値)、現在における臨界エネルギー密度
は
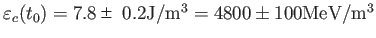 である。また、それに等価な臨界質量密度
は
である。また、それに等価な臨界質量密度
は
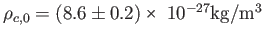 となる。
ハッブルパラメータは過去に遡るに従い、大きくなっていくので、対応する臨界
エネルギー密度も大きくなっていくことに注意しよう。さてエネルギー密度を
表すには無次元化した量を用いると都合がよい4.1。
宇宙論研究者がよく使うのは、エネルギー密度を臨界エネルギー密度で割った量、すなわち密度パラメータ
となる。
ハッブルパラメータは過去に遡るに従い、大きくなっていくので、対応する臨界
エネルギー密度も大きくなっていくことに注意しよう。さてエネルギー密度を
表すには無次元化した量を用いると都合がよい4.1。
宇宙論研究者がよく使うのは、エネルギー密度を臨界エネルギー密度で割った量、すなわち密度パラメータ
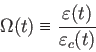 |
(4.12) |
と呼ばれる物理量である。宇宙の全エネルギーの密度パラメータが1に等しければ宇宙は平坦で
あり、1より大きければ正曲率、1より小さければ負曲率である。なお、曲率
の符号は全ての時刻で一定であることに注意しよう。空間の一様等方性と時空の
連続性を仮定する限り、宇宙の歴史の中で、曲率の符号を勝手に変化させることはできない。