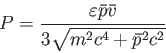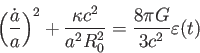2つの未知量、即ちエネルギー密度
 とスケール因子
とスケール因子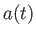 をも
つフリードマン方程式を解くには別の方程式がもう1つ必要である。今、
圧力
をも
つフリードマン方程式を解くには別の方程式がもう1つ必要である。今、
圧力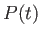 、体積
、体積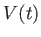 の一様なエネルギー密度をもつ物質の熱力学を考えよう。
この物質に流入する熱量を
の一様なエネルギー密度をもつ物質の熱力学を考えよう。
この物質に流入する熱量を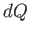 、物質の内部エネルギー変化を
、物質の内部エネルギー変化を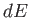 、体積変化を
、体積変化を
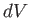 とすると、熱力学第一法則から
とすると、熱力学第一法則から
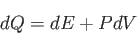 |
(4.13) |
の関係式が得られる。もし、宇宙の熱エネルギーが一様でないとすると、熱は
温度の高い部分から低い部分に流れてしまい、宇宙は非一様になってしまう。充
分大きなスケールでは宇宙は一様であるから、宇宙膨張にともなう熱の流れは存
在しないはずである。従って、流入する熱量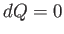 である。つまり、宇宙は断熱
膨張する。よって、
である。つまり、宇宙は断熱
膨張する。よって、
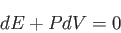 |
(4.14) |
が成立する。さて、現在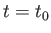 における体積を
における体積を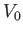 とすると、時間
とすると、時間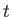 における体積は
スケール因子
における体積は
スケール因子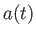 を用いて
を用いて
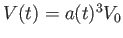 と表される。従って、
その微小変化は
と表される。従って、
その微小変化は
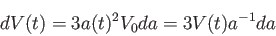 |
(4.15) |
とかける。一方、物質のエネルギー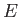 はエネルギー密度
はエネルギー密度
 を用いて
を用いて
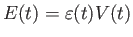 と表せる。従って、その
微小変化は
と表せる。従って、その
微小変化は
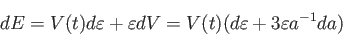 |
(4.16) |
となる。これらを断熱膨張の式に代入すると
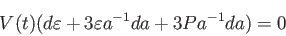 |
(4.17) |
が得られる。両辺を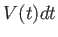 で割ると、
で割ると、
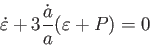 |
(4.18) |
が導ける。これを流体方程式とよぶ。
これで方程式が1つ増えたことになるが、未知数も1つ(圧力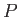 )増えたので
さらに方程式をもう1つ考えなければならない。それがエネルギー密度と圧力の関係
を表す状態方程式
)増えたので
さらに方程式をもう1つ考えなければならない。それがエネルギー密度と圧力の関係
を表す状態方程式
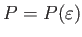 である。ここでエネルギー密度
である。ここでエネルギー密度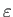 をもつ光よりじゅ
うぶんに速度が小さい質量
をもつ光よりじゅ
うぶんに速度が小さい質量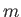 の非相対論的粒子の集団を考えよう。この粒子の集団がな
す理想気体の体積、温度、圧力、粒子数をそれぞれ
の非相対論的粒子の集団を考えよう。この粒子の集団がな
す理想気体の体積、温度、圧力、粒子数をそれぞれ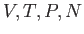 とする。すると理想
気体の状態方程式はボルツマン定数
とする。すると理想
気体の状態方程式はボルツマン定数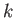 を用いて
を用いて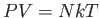 とかける。さて
とかける。さて
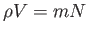 より
より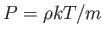 が得られる。またエネルギーと質量の等価性によ
り、
が得られる。またエネルギーと質量の等価性によ
り、
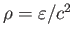 であるから、
であるから、
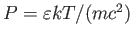 となる。さて粒子の回転の自由度が無視できると
仮定すると、エネルギー等分配則から
となる。さて粒子の回転の自由度が無視できると
仮定すると、エネルギー等分配則から
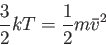 |
(4.19) |
が得られる。ここで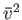 は粒子の速さの二乗平均である。この関係式を用いると、
は粒子の速さの二乗平均である。この関係式を用いると、
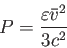 |
(4.20) |
が得られる。これが圧力とエネルギー密度の関係を表す非相対論的理想気体の
状態方程式である。一方、粒子の速さが光速に近い若しくは等しい場合、即ち相対論的理想気体の状態方程式は
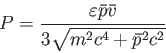 |
(4.21) |
とかける。ここで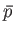 は粒子の運動量の2乗平均値の平方根である。以上よ
り、非相対論的な気体の場合は
は粒子の運動量の2乗平均値の平方根である。以上よ
り、非相対論的な気体の場合は
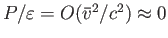 、
相対論的な気体の場合は
、
相対論的な気体の場合は
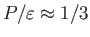 が得られる。
特に光子など質量ゼロの粒子は真空中では光速
が得られる。
特に光子など質量ゼロの粒子は真空中では光速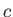 で運動するので
で運動するので
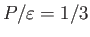 である。
ここで、圧力とエネルギー密度の比、
である。
ここで、圧力とエネルギー密度の比、
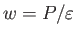 を状態方程式パラメータと呼ぶ。
宇宙スケールにおける現象を表す際、星やガスなど非相対論的物質に対して
は
を状態方程式パラメータと呼ぶ。
宇宙スケールにおける現象を表す際、星やガスなど非相対論的物質に対して
は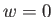 と近似すれば充分な場合が多い。
と近似すれば充分な場合が多い。
まとめると、宇宙の膨張を記述する方程式はフリードマン方程式
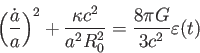 |
(4.22) |
流体方程式
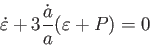 |
(4.23) |
状態方程式
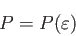 |
(4.24) |
の3つである。この3つの方程式と初期条件から3つの未知量、即ちスケール因子
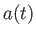 、エネルギー密度
、エネルギー密度
 、圧力
、圧力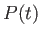 を時間の関数として求めることが出来る。
を時間の関数として求めることが出来る。