- ...
全ての銀河は一点に押し込まれていたことになる2.1
- ただし、観測者以外
の場所でも「一点」に押し込まれているので、宇宙の全ての領域がある「一点」の場所から始
まったわけではない。現在我々が観測可能な領域が「一点」に押し込まれていると考え
るべきである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
表すには無次元化した量を用いると都合がよい4.1
- 無次元であれば、プ
ランク単位系と同様に宇宙のあらゆる場所で使える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
物体が「存在」することである。6.1
-
もし、
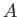 の手が十分長ければ、真っ直ぐ前に手拭い
を差し出して自分の背中を綺麗に拭うことも可能になる。鏡の場合は単に鏡に
「ぶつかって」しまうだけである。
の手が十分長ければ、真っ直ぐ前に手拭い
を差し出して自分の背中を綺麗に拭うことも可能になる。鏡の場合は単に鏡に
「ぶつかって」しまうだけである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...基本領域6.2
- 基本領域の内、中心
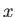 から基本領域内の点
から基本領域内の点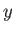 までの
最短距離
までの
最短距離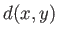 が全ての中心のコピー
が全ての中心のコピー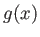 から
から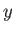 までの最短距離
までの最短距離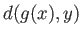 よりも小さい
よりも小さい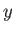 の集合から成るとき、基本領域はディリクレ領域と呼ばれる。
の集合から成るとき、基本領域はディリクレ領域と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
若干複雑だが、同様に構成出来る。6.3
- 2次元の閉曲面は全て
連続変形によって
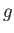 個の取っ手のついた球面に
移すことが可能である。
個の取っ手のついた球面に
移すことが可能である。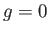 の場合は球面、
の場合は球面、
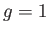 の場合は
の場合は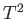 、
、
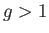 の場合は全て負の定曲率を持つ閉双曲面に移すことが出来る。
の場合は全て負の定曲率を持つ閉双曲面に移すことが出来る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...立方ラジアンである。6.4
- 閉双曲空間や球面的空間
の体積は曲率半径の3乗に比例する。通常は曲率半径が1のときの体積で「大きさ」
を表す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.