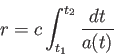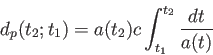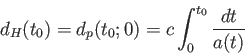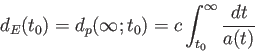宇宙は膨張しているので、2点間の距離を測るには工夫が必要である。
例えば遠方の天体が100億光年の彼方にあったとしよう。光が100億年も
かけて進む距離であれば、とんでもなく遠方であるように思えてしまうが、
宇宙膨張を考慮すると、100億年前は現在よりも天体は
我々により近い場所にあったはずである。では、どちらが正しい「距離」なのであろう
か? 実はどちらも正しい距離なのである。宇宙論的なスケールで
距離を測定する場合、2点間の事象は時間的にも離れているので、どの時点で測
定するか定義しない限り値は一意に定まらない。
いま宇宙時間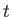 一定の面M
一定の面M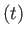 (曲率が一定)を考えよう。M
(曲率が一定)を考えよう。M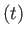 上
の2点間の距離を固有距離
上
の2点間の距離を固有距離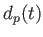 もしくは固有長という。
一方で宇宙膨張と共に膨張する座標における距離、即ち共動距離
もしくは固有長という。
一方で宇宙膨張と共に膨張する座標における距離、即ち共動距離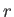 は
時間によらず不変である。宇宙時間
は
時間によらず不変である。宇宙時間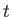 におけるスケール因子
におけるスケール因子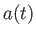 を
用いると、固有距離は
を
用いると、固有距離は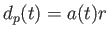 と書くことができる。つまり、固有距離は
スケール因子に比例するのである。現在はスケール因子が
と書くことができる。つまり、固有距離は
スケール因子に比例するのである。現在はスケール因子が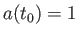 であるので
M
であるので
M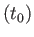 上では固有距離と共動距離が一致することに注意しよう。
さて、宇宙時間
上では固有距離と共動距離が一致することに注意しよう。
さて、宇宙時間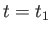 にある天体が光を発したとしよう。
その光を共動距離
にある天体が光を発したとしよう。
その光を共動距離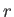 離れた観測者が
離れた観測者が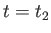 にその光を観測したと
する。さて、共動距離
にその光を観測したと
する。さて、共動距離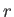 の値はどうやって計算すればよいのだろうか?
ナイーブには距離=光速×時間であるから
の値はどうやって計算すればよいのだろうか?
ナイーブには距離=光速×時間であるから
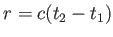 と考えるかもしれない。
もし、宇宙が「静止」していれば確かにそうなるであろう。しかし、宇宙は膨張
しているため、ナイーブに求められた式は正しくない。観測者を原点に置いた極
座標を考えよう。光は
と考えるかもしれない。
もし、宇宙が「静止」していれば確かにそうなるであろう。しかし、宇宙は膨張
しているため、ナイーブに求められた式は正しくない。観測者を原点に置いた極
座標を考えよう。光は
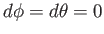 である
である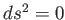 のヌル測地線に沿って
運動する。従って、ヌル測地線に沿って
のヌル測地線に沿って
運動する。従って、ヌル測地線に沿って
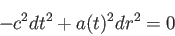 |
(6.1) |
つまり、
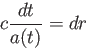 |
(6.2) |
が成立する。両辺を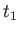 から
から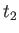 まで積分すると
まで積分すると
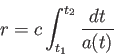 |
(6.3) |
が得られる。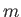 を定数として
を定数として
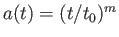 とかけるとき、
とかけるとき、
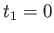 で
で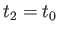 かつ
かつ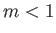 であれば
であれば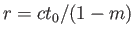 となる。この場合、
となる。この場合、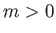 であればナイーブに求められた値に比べて増大していることになる。これは宇宙膨張の効
果によるものである。グローバルな光の運動を考えるのであれば、距離を経過時
間で割った「光の平均速さ」は光速を超えられるのである。
固有距離はこのようにして求まった共動距離にスケール因子をかければよい。
例えば、M
であればナイーブに求められた値に比べて増大していることになる。これは宇宙膨張の効
果によるものである。グローバルな光の運動を考えるのであれば、距離を経過時
間で割った「光の平均速さ」は光速を超えられるのである。
固有距離はこのようにして求まった共動距離にスケール因子をかければよい。
例えば、M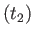 における固有距離は
における固有距離は
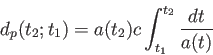 |
(6.4) |
となる(セミコロン以下の変数は光を発した宇宙時間を表す)。
さて現在における宇宙M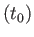 における固有距離の最大値はどれくらいであろうか?
宇宙が宇宙時間
における固有距離の最大値はどれくらいであろうか?
宇宙が宇宙時間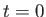 で特異点即ち密度が発散する点から始まったと仮定する。
このときスケール因子は
で特異点即ち密度が発散する点から始まったと仮定する。
このときスケール因子は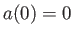 であろう。スケール因子
であろう。スケール因子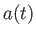 は常に正である
ので現在における固有距離は光が
は常に正である
ので現在における固有距離は光が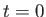 にときに発した時最大となる。
この固有距離の値
にときに発した時最大となる。
この固有距離の値
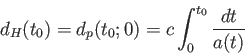 |
(6.5) |
をとる地点を現在における粒子ホライズンと呼ぶ。我々から共動距離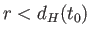 にある
全ての天体と我々は過去に因果関係をもったことになる。いいかえる
と、粒子ホライズンは我々が今までに「みえた」範囲の境界を表すのである。
又、現在から未来に向かってある時間の後、我々と因果関係をもつことができる
地点の固有距離の最大値は
にある
全ての天体と我々は過去に因果関係をもったことになる。いいかえる
と、粒子ホライズンは我々が今までに「みえた」範囲の境界を表すのである。
又、現在から未来に向かってある時間の後、我々と因果関係をもつことができる
地点の固有距離の最大値は
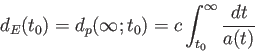 |
(6.6) |
である。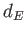 の距離にある地点を現在における事象ホライズンもしく
はイベントホライズンと呼び、これから「みえるであろう」範囲の境界を表す。
事象ホライズンは観測者の運動状態によるため、事象ホライズンを恣意的に変えることは
可能である。しかし、過去の事象で決まる粒子ホライズンは変えることができな
い。
の距離にある地点を現在における事象ホライズンもしく
はイベントホライズンと呼び、これから「みえるであろう」範囲の境界を表す。
事象ホライズンは観測者の運動状態によるため、事象ホライズンを恣意的に変えることは
可能である。しかし、過去の事象で決まる粒子ホライズンは変えることができな
い。