遠方の天体までの固有距離を直接測定することは非常に難しい。なぜなら、天体
が光を発した時刻と我々が観測する時刻は大きく異なり、その間に宇宙は膨張し
てしまうからである。観測値が同じでも、膨張の様子が違えば、固有距離も違っ
てしまうであろう。とりあえず宇宙は平坦で静止していると考え、観測値から
直接決まる様々な「距離」を定義すると便利である。その1つに天体の明るさ、
すなわち光度(単位W)を用いる光度距離がある。いま、光度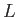 が既知であ
る標準光源Sを考えよう。簡単のため、Sは等方に光を発しているとする。観測者が受
け取る光のフラックス、即ち単位面積当たり単位時間に受け取る光のエネルギー
が既知であ
る標準光源Sを考えよう。簡単のため、Sは等方に光を発しているとする。観測者が受
け取る光のフラックス、即ち単位面積当たり単位時間に受け取る光のエネルギー
![$f[\textrm{W}/\textrm{m}^2]$](img528.png) は、光源Sまでの「距離」を
は、光源Sまでの「距離」を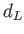 とすると、空間
が平坦であれば、
とすると、空間
が平坦であれば、
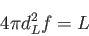 |
(6.7) |
を満たす。即ち、
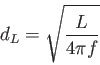 |
(6.8) |
であるが、この式で定義される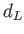 が光度距離である。
が光度距離である。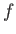 は観測量であるから、
は観測量であるから、
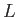 さえ決まっていれば、宇宙モデルによらず、計算することが出来る。
宇宙が膨張していたり、空間的に曲率をもつ、すなわち時空が歪んでいる場合は
一般的に光度距離と固有距離が等しくならないことに注意しよう。
さえ決まっていれば、宇宙モデルによらず、計算することが出来る。
宇宙が膨張していたり、空間的に曲率をもつ、すなわち時空が歪んでいる場合は
一般的に光度距離と固有距離が等しくならないことに注意しよう。
原因は2つある。第1の原因は、時間の伸びの効果である。
FRW宇宙を考え、スケール因子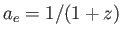 のときに、その天体が静止している系
で
のときに、その天体が静止している系
で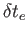 の時間間隔で天体が光を出したとしよう。我々が観測する光の時間間
隔は
の時間間隔で天体が光を出したとしよう。我々が観測する光の時間間
隔は
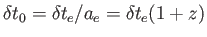 となる。つまり、光の時間
間隔は長くなる。これは遠方の天体はスローモーションで動いているようにみえ
ることを表している。さらに、静止系における各光子のエネルギー
となる。つまり、光の時間
間隔は長くなる。これは遠方の天体はスローモーションで動いているようにみえ
ることを表している。さらに、静止系における各光子のエネルギー
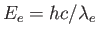 は、
赤方偏移により
は、
赤方偏移により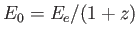 であると観測される。これも遠方の天体がスローモーションで振動しているためである。
一方、観測されるフラックス
であると観測される。これも遠方の天体がスローモーションで振動しているためである。
一方、観測されるフラックス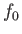 は光子のエネルギーに比例し、時
間間隔に反比例するので、もとのフラックス
は光子のエネルギーに比例し、時
間間隔に反比例するので、もとのフラックス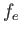 に比べ減少する。即ち
に比べ減少する。即ち
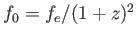 と
なる。よって光度距離は
と
なる。よって光度距離は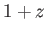 に比例する。
に比例する。
第2の原因は、空間の曲がりの効果である。観測者を原点にとり、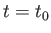 におい
て固有距離
におい
て固有距離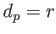 一定として得られる2次元球面を考える。このとき球面の表面
積は
一定として得られる2次元球面を考える。このとき球面の表面
積は
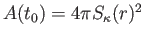 で表される。ここで
で表される。ここで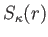 は
は
である。従って、球面積を半径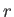 の2乗で割って得られる全立体角
の2乗で割って得られる全立体角
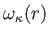 は
は
となる。一般に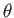 を任意の角度とすると
を任意の角度とすると
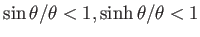 より、全立体角
より、全立体角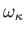 は空間のガウス曲率が正ならば
は空間のガウス曲率が正ならば
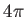 より小さく、負ならば
より小さく、負ならば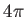 より大きい。いいかえると、光子が拡がる
面積は、前者の場合小さく、後者の場合大きくなるのである。観測されるフラッ
クスは球面積に反比例するので、空間のガウス曲率が正ならば
フラックスは大きく、負ならば小さくなる。つまり、空間の曲率を考慮すると、
より大きい。いいかえると、光子が拡がる
面積は、前者の場合小さく、後者の場合大きくなるのである。観測されるフラッ
クスは球面積に反比例するので、空間のガウス曲率が正ならば
フラックスは大きく、負ならば小さくなる。つまり、空間の曲率を考慮すると、
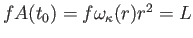 であるから、
であるから、
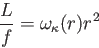 |
(6.9) |
が成り立つ。結局、光度距離は において
において
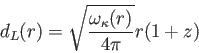 |
(6.10) |
と表せる。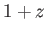 は時間の伸びの効果、
は時間の伸びの効果、
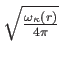 は
空間の曲がりの効果を表す。
は
空間の曲がりの効果を表す。
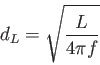
![]() のときに、その天体が静止している系
で
のときに、その天体が静止している系
で![]() の時間間隔で天体が光を出したとしよう。我々が観測する光の時間間
隔は
の時間間隔で天体が光を出したとしよう。我々が観測する光の時間間
隔は
![]() となる。つまり、光の時間
間隔は長くなる。これは遠方の天体はスローモーションで動いているようにみえ
ることを表している。さらに、静止系における各光子のエネルギー
となる。つまり、光の時間
間隔は長くなる。これは遠方の天体はスローモーションで動いているようにみえ
ることを表している。さらに、静止系における各光子のエネルギー
![]() は、
赤方偏移により
は、
赤方偏移により![]() であると観測される。これも遠方の天体がスローモーションで振動しているためである。
一方、観測されるフラックス
であると観測される。これも遠方の天体がスローモーションで振動しているためである。
一方、観測されるフラックス![]() は光子のエネルギーに比例し、時
間間隔に反比例するので、もとのフラックス
は光子のエネルギーに比例し、時
間間隔に反比例するので、もとのフラックス![]() に比べ減少する。即ち
に比べ減少する。即ち
![]() と
なる。よって光度距離は
と
なる。よって光度距離は![]() に比例する。
に比例する。
![]() におい
て固有距離
におい
て固有距離![]() 一定として得られる2次元球面を考える。このとき球面の表面
積は
一定として得られる2次元球面を考える。このとき球面の表面
積は
![]() で表される。ここで
で表される。ここで![]() は
は
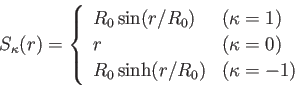
![\begin{eqnarray*}
\omega_\kappa(r)=\left\{
\begin{array}{lll}
4 \pi [\sin(r/R_0)...
...4 \pi [\sinh(r/R_0)/(r/R_0)]^2 & (\kappa=-1)
\end{array} \right.
\end{eqnarray*}](img547.png)
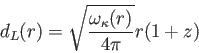
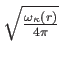 は
空間の曲がりの効果を表す。
は
空間の曲がりの効果を表す。