光度の代わりに 標準ものさしを基準にして距離を定義することも出来
る。いま、固有長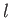 が既知の天体を考える。光度距離の場合と同様、宇宙は平
坦で静止していると仮定する。天体までの距離は充分遠いため天体を見込む角度
が既知の天体を考える。光度距離の場合と同様、宇宙は平
坦で静止していると仮定する。天体までの距離は充分遠いため天体を見込む角度
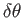 は大変小さい(
は大変小さい(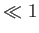 )と仮定しよう。すると、天体までの距
離
)と仮定しよう。すると、天体までの距
離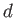 は
は
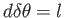 を満たす。つまり、
を満たす。つまり、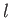 と観測量
と観測量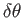 を用いて距離を求めることが出来る。同様に曲がった膨張宇宙の場合にも同じ定
義を用いた場合、その距離
を用いて距離を求めることが出来る。同様に曲がった膨張宇宙の場合にも同じ定
義を用いた場合、その距離
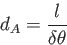 |
(6.11) |
を角径距離と呼ぶ。FRWモデルにおいて赤方偏移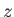 の天体までの
角径距離は、天体を中心とし、観測者を含む
共動半径
の天体までの
角径距離は、天体を中心とし、観測者を含む
共動半径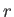 の球面の全立体角
の球面の全立体角
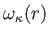 を用いて
を用いて
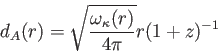 |
(6.12) |
と表せる。その理由は以下の通りである。光度距離の場合と同様に
観測者を中心とする球座標系
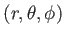 を取ってみよう。
光は
を取ってみよう。
光は
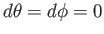 を満たすヌル測地線に沿って観測者に到達する。
今、天体の幅を見込む角度が
を満たすヌル測地線に沿って観測者に到達する。
今、天体の幅を見込む角度が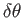 であったとしよう。すると
天体が光を発した時刻が
であったとしよう。すると
天体が光を発した時刻が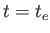 のとき、
のとき、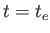 面における天体の幅、
即ち固有距離は
面における天体の幅、
即ち固有距離は
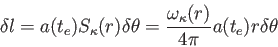 |
(6.13) |
である。
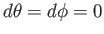 より、現在
より、現在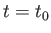 に到るまで、天体の幅を見込む
角度
に到るまで、天体の幅を見込む
角度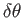 は変化しない。従って、
は変化しない。従って、
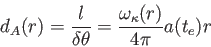 |
(6.14) |
となり、
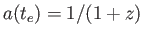 より、式(6.12)が得られる。
宇宙が平坦な場合
より、式(6.12)が得られる。
宇宙が平坦な場合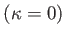 、角径距離は天体は光を発した時間一定面におけ
る固有距離に等しい。即ち
、角径距離は天体は光を発した時間一定面におけ
る固有距離に等しい。即ち
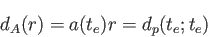 |
(6.15) |
である。標準宇宙モデルでは、角径距離は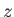 がある程度以上大きくなると、減
少し始める。つまり、より古い天体ほど見かけの大きさが大きくなる。
いいかえると、「遠い」天体ほど近くにあるようにみえるのである。
しかし、光度距離は
がある程度以上大きくなると、減
少し始める。つまり、より古い天体ほど見かけの大きさが大きくなる。
いいかえると、「遠い」天体ほど近くにあるようにみえるのである。
しかし、光度距離は
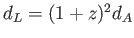 を満たすので、明るさは常に減少する。
これら一見不思議な効果は全て時空の歪みに起因する。
を満たすので、明るさは常に減少する。
これら一見不思議な効果は全て時空の歪みに起因する。