宇宙膨張を測定するには「ものさし」となる物理量が必要である。
例えば、光度距離を測るためには、測定される光源の元々の
明るさが分かっていなければならない。例えば、100Wの電球であれば、
そのみかけの明るさから電球までの光度距離が分かる。残念ながら、宇宙には100Wの
電球のように元々の明るさが分かっている光源は数少ない。しかし、ある種の天
体では別の物理量からその元々の明るさを測定できる。その1つがIa型超新星で
ある。超新星とはおおざっぱに言えば、突然爆発的に明るくなる星のことである。
白色矮星と呼ばれる温度の高いコンパクトな天体にその伴星のガスが流入することがその爆発的増光の原因であると考えられている。
白色矮星は電子の縮退圧によって莫大な重力を支えているが、さらに質量が降り
積もることにより、重力を支えきれなくなるためである。Ia型超新星は増光時に
おける明るさが明るいほど、暗くなるまでの期間が
長くなるという性質があるため、減光するまでの時間を測定することによって、
元々の明るさを推定できる。実際には、絶対的な明るさ(ある一定の光度距離に
おける明るさ)がよく分かっている近傍の様々なIa型超新星の解析から
光度の時間変化のテンプレートをいくつか作成し、遠方のIa型超新星の性質と
同じであるという仮定の下、観測された光度の時間変化にもっともよく合うテンプレー
トを用いることにより、絶対的な明るさを推定する。
見かけの明るさは観測される光のフラックス、すなわち単位面積を単位時間に通
過する光のエネルギーで測ることができる。単位は[W/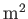 ]である。
しかし、天文学者はSI単位系よりも伝統的な単位である「等級」を用いることが
多い。月の無い暗い夜空で肉眼でやっと見える星の明るさを6等級とし、
1等級の星は6等級の100倍の明るさをもっていると定義するのである。
つまり5等変化すると100倍、1等変化すると
]である。
しかし、天文学者はSI単位系よりも伝統的な単位である「等級」を用いることが
多い。月の無い暗い夜空で肉眼でやっと見える星の明るさを6等級とし、
1等級の星は6等級の100倍の明るさをもっていると定義するのである。
つまり5等変化すると100倍、1等変化すると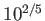 倍明るくなるという単位
系である。SI単位系におけるフラックス
倍明るくなるという単位
系である。SI単位系におけるフラックス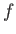 とそれに対応する見かけの等級
とそれに対応する見かけの等級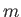 の
関係は
の
関係は
![\begin{displaymath}
m \equiv -2.5 \log_{10}\biggl[f/(2.53\times 10^{-8}\textrm{W}/\textrm{m}^2
)\biggr ]
\end{displaymath}](img571.png) |
(6.16) |
で表される。光源である天体までの距離が変われば当然みかけの明るさは
変化する。したがって、その天体の絶対的明るさを表すには、その天体から観測
者までの距離を一定にしなければならない。仮に光源までの光度距離が10pcで
あったとしよう。このときの見かけの等級を絶対等級と呼び、
Mで表す。等級は明るさの対数に対応するため、等級の変化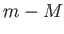 がどれだけ天体が
暗くなったかを表すことになる。暗くなるということは距離が大きくなっている
ことを示すため、
がどれだけ天体が
暗くなったかを表すことになる。暗くなるということは距離が大きくなっている
ことを示すため、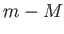 は距離指数とも呼ばれている。観測量である距
離指数と光度距離の関係を考えてみよう。光度距離
は距離指数とも呼ばれている。観測量である距
離指数と光度距離の関係を考えてみよう。光度距離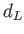 の天体のみかけの等級
が
の天体のみかけの等級
が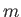 であり、観測者が受け取るフラックスが
であり、観測者が受け取るフラックスが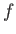 であったとする。定義から観測
者が受け取るフラックスは光度距離
であったとする。定義から観測
者が受け取るフラックスは光度距離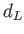 の2乗に反比例するため、
の2乗に反比例するため、
![\begin{displaymath}
M = -2.5 \log_{10}\biggl[f\times (10\textrm{pc})^2/(d_L^2 \times 2.53\times 10^{-8}\textrm{W}/\textrm{m}^2
)\biggr ]
\end{displaymath}](img573.png) |
(6.17) |
である。従って、
![\begin{displaymath}
m-M=5 \log_{10}\biggl[ \frac{d_L}{10 \textrm{pc}}\biggr]
\end{displaymath}](img574.png) |
(6.18) |
又は、
![\begin{displaymath}
m-M=5 \log_{10}\biggl[ \frac{d_L}{1 \textrm{Mpc}}\biggr]+25
\end{displaymath}](img575.png) |
(6.19) |
と表される。例えば、100Mpc離れた天体は10pcの場合に比べ35等級暗くなる。
これにより観測量である距離指数から光度距離を求めることが可能になる。
Ia型超新星の所属している銀河の光を分光器にかけ、銀河のガスによる
吸収線や輝線の波長を観測することにより、銀河の赤方偏移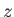 を測ることが出
来る。Ia型超新星の赤方偏移が所属している銀河の赤方偏移とほぼ
同じであると仮定すれば、赤方偏移
を測ることが出
来る。Ia型超新星の赤方偏移が所属している銀河の赤方偏移とほぼ
同じであると仮定すれば、赤方偏移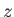 と距離指数
と距離指数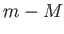 の関係を観測的に求めることが
出来る。一方、宇宙モデルを仮定すれば、様々な天体の赤方偏移
の関係を観測的に求めることが
出来る。一方、宇宙モデルを仮定すれば、様々な天体の赤方偏移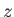 と天体までの
光度距離
と天体までの
光度距離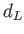 即ち距離指数
即ち距離指数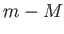 の関係を求めることができる。よって、観測さ
れた
の関係を求めることができる。よって、観測さ
れた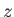 と
と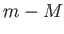 の関係をもっとも良く説明する宇宙論パラメーターを決定すること
が出来る。
の関係をもっとも良く説明する宇宙論パラメーターを決定すること
が出来る。
Ia型超新星の赤方偏移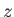 がそれほど大きくない
がそれほど大きくない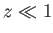 の場合を考えよう。
このとき、光源までの光度距離は近似的にスケール因子の1階微分と2階微分を
用いて表すことが出来る。すなわち、
の場合を考えよう。
このとき、光源までの光度距離は近似的にスケール因子の1階微分と2階微分を
用いて表すことが出来る。すなわち、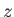 の2次までの近似では
の2次までの近似では
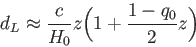 |
(6.20) |
とかける。ここで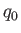 は減速パラメータと呼ばれ、現在
は減速パラメータと呼ばれ、現在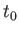 において
において
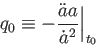 |
(6.21) |
で定義され、宇宙の減速率を特徴付ける無次元のパラメータである。
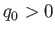 であれば、宇宙は減速膨張
であれば、宇宙は減速膨張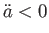 、
、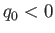 であれば、宇宙は加速
膨張
であれば、宇宙は加速
膨張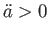 である。
である。
Ia型超新星の観測結果から、我々の宇宙の減速パラメータ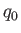 は負、すなわち
宇宙は現在加速していることが判明した。この業績により、Perlmutter,
Schimidt, Riessの3人の宇宙物理学者は2011年度ノーベル物理学賞を受賞した。
は負、すなわち
宇宙は現在加速していることが判明した。この業績により、Perlmutter,
Schimidt, Riessの3人の宇宙物理学者は2011年度ノーベル物理学賞を受賞した。
図 6.1:
Ia型超新星の距離指数と赤方偏移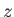 の関係。(Perlmutter et
al. 1999, ApJ, 517, 565-58 から引用。)
の関係。(Perlmutter et
al. 1999, ApJ, 517, 565-58 から引用。)
![\includegraphics[width=160mm]{hubble-diagram.eps}](img582.png) |
図 6.2:
様々な
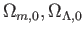 に対する観測データ
へのフィッティング。(Perlmutter et
al. 1999, ApJ, 517, 565-58 から引用。)
に対する観測データ
へのフィッティング。(Perlmutter et
al. 1999, ApJ, 517, 565-58 から引用。)
![\includegraphics[width=160mm]{q0-diagram.eps}](img583.png) |
![]() ]である。
しかし、天文学者はSI単位系よりも伝統的な単位である「等級」を用いることが
多い。月の無い暗い夜空で肉眼でやっと見える星の明るさを6等級とし、
1等級の星は6等級の100倍の明るさをもっていると定義するのである。
つまり5等変化すると100倍、1等変化すると
]である。
しかし、天文学者はSI単位系よりも伝統的な単位である「等級」を用いることが
多い。月の無い暗い夜空で肉眼でやっと見える星の明るさを6等級とし、
1等級の星は6等級の100倍の明るさをもっていると定義するのである。
つまり5等変化すると100倍、1等変化すると![]() 倍明るくなるという単位
系である。SI単位系におけるフラックス
倍明るくなるという単位
系である。SI単位系におけるフラックス![]() とそれに対応する見かけの等級
とそれに対応する見かけの等級![]() の
関係は
の
関係は
![]() がそれほど大きくない
がそれほど大きくない![]() の場合を考えよう。
このとき、光源までの光度距離は近似的にスケール因子の1階微分と2階微分を
用いて表すことが出来る。すなわち、
の場合を考えよう。
このとき、光源までの光度距離は近似的にスケール因子の1階微分と2階微分を
用いて表すことが出来る。すなわち、![]() の2次までの近似では
の2次までの近似では
![]() は負、すなわち
宇宙は現在加速していることが判明した。この業績により、Perlmutter,
Schimidt, Riessの3人の宇宙物理学者は2011年度ノーベル物理学賞を受賞した。
は負、すなわち
宇宙は現在加速していることが判明した。この業績により、Perlmutter,
Schimidt, Riessの3人の宇宙物理学者は2011年度ノーベル物理学賞を受賞した。