次に、平坦で、物質と宇宙定数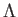 をもつ2成分FRWモデルを考えよう。
物質+
をもつ2成分FRWモデルを考えよう。
物質+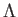 モデルは現在に近い時代における宇宙膨張をもっとも正しく表すモデルと考え
られている。
モデルは現在に近い時代における宇宙膨張をもっとも正しく表すモデルと考え
られている。
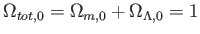 で
で
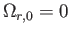 である
から、式(5.17)は
である
から、式(5.17)は
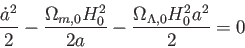 |
(5.20) |
とかける。さて、式(5.20)で重力ポテンシャルを表すのは
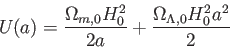 |
(5.21) |
である。まず
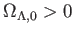 の場合を考えよう。このとき
の場合を考えよう。このとき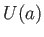 は
は
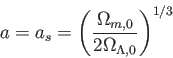 |
(5.22) |
で極大値
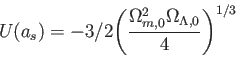 |
(5.23) |
をとる。しかし、
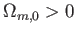 に対し
に対し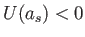 であるので、力学的エネル
ギー
であるので、力学的エネル
ギー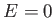 すなわち、平坦な宇宙ではこのポテンシャル
すなわち、平坦な宇宙ではこのポテンシャル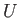 の壁を乗り越えることが
できる。つまり、宇宙は永遠に膨張する(ビッグチル)。次に
の壁を乗り越えることが
できる。つまり、宇宙は永遠に膨張する(ビッグチル)。次に
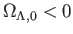 の場合を考えよう。このとき、ポテンシャル
の場合を考えよう。このとき、ポテンシャル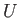 は
は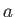 と
共に単調増加するので、ポテンシャル
と
共に単調増加するので、ポテンシャル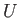 の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまりビッ
グクランチを迎える。
もう少し具体的に調べるため、
の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまりビッ
グクランチを迎える。
もう少し具体的に調べるため、
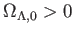 の場合の解
の場合の解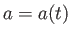 を求めてみよう。質量密度は
を求めてみよう。質量密度は
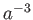 に比例するので宇宙初期に質量密度が優勢でも時間の経過と共に密度が薄くな
り、宇宙のエネルギーに占める宇宙定数
に比例するので宇宙初期に質量密度が優勢でも時間の経過と共に密度が薄くな
り、宇宙のエネルギーに占める宇宙定数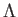 の相対的寄与が大きくなっていく。今、質量と宇宙定数
の密度がそれぞれ等しくなる質量-
の相対的寄与が大きくなっていく。今、質量と宇宙定数
の密度がそれぞれ等しくなる質量-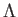 同値時刻時刻
同値時刻時刻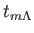 におけるスケール因子を
におけるスケール因子を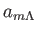 としよう。簡単な計算から
としよう。簡単な計算から
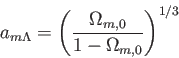 |
(5.24) |
が得られる。
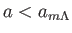 では質量密度が、
では質量密度が、
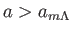 では
では
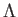 が優勢である。式(5.17)で
が優勢である。式(5.17)で
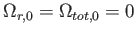 とおき、積分すると
とおき、積分すると
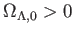 に対し、
に対し、
![\begin{displaymath}
H_0 t=\frac {2}{3\sqrt{1-\Omega_{m,0}}}\ln \Biggl[
\Biggl(\f...
...}+\sqrt{1+
\Biggl(\frac {a}{a_{m\Lambda}} \Biggr)^{3}}
\Biggr]
\end{displaymath}](img445.png) |
(5.25) |
となる。これの逆関数を求めることにより、スケール因子の時間発展
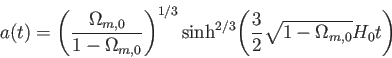 |
(5.26) |
が得られる。近年の観測データ(Planck+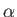 2013)から求められたベストフィット値
2013)から求められたベストフィット値
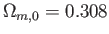 、
、
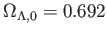 、
、
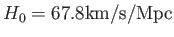 を用いると、質量-
を用いると、質量-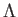 同値時刻におけるスケール因子は
同値時刻におけるスケール因子は
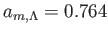 、
、
 の時刻を0としたときの現在時刻(宇宙年齢)は
の時刻を0としたときの現在時刻(宇宙年齢)は
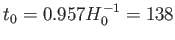 億年となる。質量-
億年となる。質量-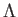 同値時刻は
同値時刻は
![\begin{displaymath}
t_{m\Lambda}=\frac {2H_0^{-1}}{3 \sqrt{1-\Omega_{m,0}}} \ln\Biggl[1+\sqrt{2}
\Biggr]=0.7063H_0^{-1}=102億年
\end{displaymath}](img453.png) |
(5.27) |
となり、平坦な質量-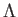 宇宙モデルが正しければ、宇宙は生まれてから102億年
の間は質量優勢(
宇宙モデルが正しければ、宇宙は生まれてから102億年
の間は質量優勢(
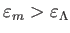 )、その後36億年の間は
)、その後36億年の間は
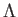 優勢(
優勢(
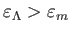 )であったことになる。
)であったことになる。
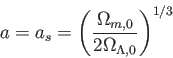
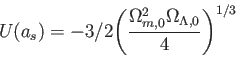
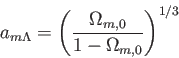
![\begin{displaymath}
H_0 t=\frac {2}{3\sqrt{1-\Omega_{m,0}}}\ln \Biggl[
\Biggl(\f...
...}+\sqrt{1+
\Biggl(\frac {a}{a_{m\Lambda}} \Biggr)^{3}}
\Biggr]
\end{displaymath}](img445.png)
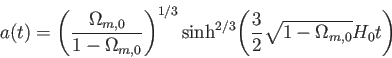
![\begin{displaymath}
t_{m\Lambda}=\frac {2H_0^{-1}}{3 \sqrt{1-\Omega_{m,0}}} \ln\Biggl[1+\sqrt{2}
\Biggr]=0.7063H_0^{-1}=102億年
\end{displaymath}](img453.png)