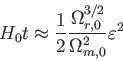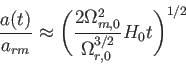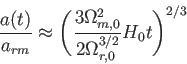我々の宇宙には物質だけでなく輻射成分も含まれている。輻射成分のエネルギー
密度はスケール因子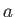 の4乗に反比例するため、宇宙初期において質量や宇宙定
数
の4乗に反比例するため、宇宙初期において質量や宇宙定
数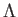 に比べ優勢であるはずである。輻射成分を採り入れると、
平坦な質量-
に比べ優勢であるはずである。輻射成分を採り入れると、
平坦な質量-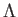 宇宙モデルを用いた宇宙年齢にどれほど影響を及ぼすので
あろうか?
宇宙モデルを用いた宇宙年齢にどれほど影響を及ぼすので
あろうか?
宇宙の輻射成分として考えられるのは光子であるが、宇宙初期ではニュートリノ
も輻射成分として考える必要がある。それはなぜだろうか?
ニュートリノの質量の大きさは不明であるがその値は電子や陽子に比べ
非常に小さい(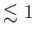 eV)と考えられている。
したがって、高温の宇宙初期においてニュートリノは電子や陽子と同じく光速に近い速
さで運動し、弱い相互作用をしながら様々な粒子と衝突を繰り返している。この
時代では全ての粒子は見分けがつかず、宇宙の温度
eV)と考えられている。
したがって、高温の宇宙初期においてニュートリノは電子や陽子と同じく光速に近い速
さで運動し、弱い相互作用をしながら様々な粒子と衝突を繰り返している。この
時代では全ての粒子は見分けがつかず、宇宙の温度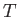 で表される熱平衡状態に
ある。
で表される熱平衡状態に
ある。
しかし、宇宙膨張と共に粒子の密度が下がっていくと、他の粒子に出会うチャン
スが少なくなり、熱平衡状態を保つことが困難になってくる。ニュートリノは
電磁相互作用に比べ、非常に「弱い」相互作用(いわゆる弱い相互作用)しか
しないため、宇宙の温度が比較的高い(
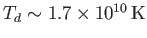 )時期にプラズマ状態にある粒子の集団から外れてしまう(脱結合)。
この脱結合時の温度が電子の質量エネルギーに対応する温度
)時期にプラズマ状態にある粒子の集団から外れてしまう(脱結合)。
この脱結合時の温度が電子の質量エネルギーに対応する温度
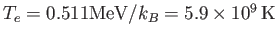 よりも大きいため、電子は依
然として光速に近い速さで運動しているが、その後、宇宙の温度が下がっていく
と、やがて電子の速度が光速よりも遅くなり、電子と陽電子が衝突して対消滅し、光子
ができる反応によって、ほとんどの電子と陽電子が消えてしまう。この対消滅に
伴って新しく生まれる光子による「加熱」のため、熱平衡状態にあるプラズマ粒子の
温度の低下は幾分か抑えられる。一方、ニュートリノはもはや電子や光子と
相互作用しないので、新しく生まれた光子による「加熱」は期待できない。する
とニュートリノの「温度」は光子の温度より下がってしまうのである。
よりも大きいため、電子は依
然として光速に近い速さで運動しているが、その後、宇宙の温度が下がっていく
と、やがて電子の速度が光速よりも遅くなり、電子と陽電子が衝突して対消滅し、光子
ができる反応によって、ほとんどの電子と陽電子が消えてしまう。この対消滅に
伴って新しく生まれる光子による「加熱」のため、熱平衡状態にあるプラズマ粒子の
温度の低下は幾分か抑えられる。一方、ニュートリノはもはや電子や光子と
相互作用しないので、新しく生まれた光子による「加熱」は期待できない。する
とニュートリノの「温度」は光子の温度より下がってしまうのである。
詳しい計算によると脱結合以降のニュートリノの温度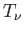 は光子の温度
は光子の温度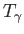 を用いて
を用いて
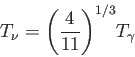 |
(5.28) |
と表せる。また、3種類あるニュートリノ
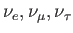 の
各エネルギー密度
の
各エネルギー密度
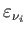 は光子のエネルギー密度
は光子のエネルギー密度
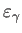 を用いてそれぞれ
を用いてそれぞれ
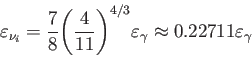 |
(5.29) |
と表せる。つまり、全輻射密度パラメータは光子の密度パラメータを用いて
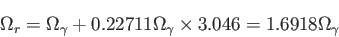 |
(5.30) |
とかける。ここでニュートリノの種類の数である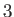 ではなく、
ではなく、
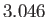 をかけているのは、ニュートリノが脱結合する際の非平衡過程の効果を
採り入れているためである。さて、光子の密度パラメータはCMBの温度
をかけているのは、ニュートリノが脱結合する際の非平衡過程の効果を
採り入れているためである。さて、光子の密度パラメータはCMBの温度
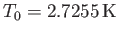 より、
より、
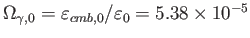 と求まるので、結局
と求まるので、結局
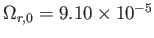 となる。
つまり、現在、輻射エネルギーの寄与は質量エネルギーの約1/3400となり、大変小さい
ことが分かる。
となる。
つまり、現在、輻射エネルギーの寄与は質量エネルギーの約1/3400となり、大変小さい
ことが分かる。
しかし、過去に向かって時間を遡ると、輻射エネルギー密度と質量エネルギー密
度の比は段々大きくなり、ついにある時刻において両者は同じになる。
この時刻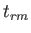 を輻射質量等価時と呼ぶ。
を輻射質量等価時と呼ぶ。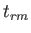 におけるスケール因子は
におけるスケール因子は
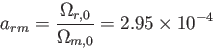 |
(5.31) |
で与えられる。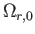 は非常に小さいため、輻射と質量のエネルギー密
度の寄与が同じくらいの時代において宇宙定数
は非常に小さいため、輻射と質量のエネルギー密
度の寄与が同じくらいの時代において宇宙定数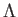 の寄与はほとんど無視できる。
従って、質量と輻射を含む2成分モデルを考えれば充分である。
宇宙が平坦であると仮定すると、宇宙時間
の寄与はほとんど無視できる。
従って、質量と輻射を含む2成分モデルを考えれば充分である。
宇宙が平坦であると仮定すると、宇宙時間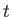 は式(5.18)より、
は式(5.18)より、
で与えられる。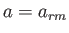 を代入すると、
を代入すると、
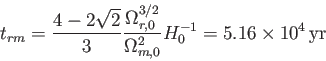 |
(5.33) |
が得られる。つまり、輻射エネルギーの寄与が他の成分に比べ
大きかった期間は宇宙が始まって以来、高々5万年程度である。この値は質量-宇宙定数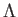 モデルで求めた宇宙年齢
(138億年)に比べ遙かに小さいため、宇宙年齢を高々3桁程度の精度で計算するた
めであれば、輻射の影響は考慮しなくてもよいことが分かる。
モデルで求めた宇宙年齢
(138億年)に比べ遙かに小さいため、宇宙年齢を高々3桁程度の精度で計算するた
めであれば、輻射の影響は考慮しなくてもよいことが分かる。
さて式(5.32)の右辺から得られる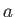 に関する3次方程式を解くこと
により、スケール因子
に関する3次方程式を解くこと
により、スケール因子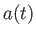 が宇宙時間
が宇宙時間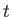 の関数として求まる。しかし、やや複雑な表式になるので、
ここでは輻射優勢時(
の関数として求まる。しかし、やや複雑な表式になるので、
ここでは輻射優勢時(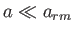 )と質量優勢時(
)と質量優勢時(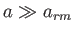 )の二つの時代に分けて宇宙膨張
を考えよう。
)の二つの時代に分けて宇宙膨張
を考えよう。
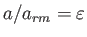 とおくと、
とおくと、
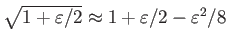 より、
より、
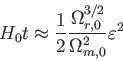 |
(5.34) |
となるので、輻射優勢時(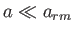 )では
)では
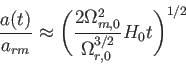 |
(5.35) |
となる。前節で導出した通り、
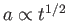 が確かめられる。
同様に、質量優勢時(
が確かめられる。
同様に、質量優勢時(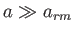 )では
)では
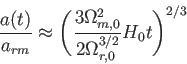 |
(5.36) |
となる。つまり、
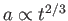 である。
である。
![]() eV)と考えられている。
したがって、高温の宇宙初期においてニュートリノは電子や陽子と同じく光速に近い速
さで運動し、弱い相互作用をしながら様々な粒子と衝突を繰り返している。この
時代では全ての粒子は見分けがつかず、宇宙の温度
eV)と考えられている。
したがって、高温の宇宙初期においてニュートリノは電子や陽子と同じく光速に近い速
さで運動し、弱い相互作用をしながら様々な粒子と衝突を繰り返している。この
時代では全ての粒子は見分けがつかず、宇宙の温度![]() で表される熱平衡状態に
ある。
で表される熱平衡状態に
ある。
![]() )時期にプラズマ状態にある粒子の集団から外れてしまう(脱結合)。
この脱結合時の温度が電子の質量エネルギーに対応する温度
)時期にプラズマ状態にある粒子の集団から外れてしまう(脱結合)。
この脱結合時の温度が電子の質量エネルギーに対応する温度
![]() よりも大きいため、電子は依
然として光速に近い速さで運動しているが、その後、宇宙の温度が下がっていく
と、やがて電子の速度が光速よりも遅くなり、電子と陽電子が衝突して対消滅し、光子
ができる反応によって、ほとんどの電子と陽電子が消えてしまう。この対消滅に
伴って新しく生まれる光子による「加熱」のため、熱平衡状態にあるプラズマ粒子の
温度の低下は幾分か抑えられる。一方、ニュートリノはもはや電子や光子と
相互作用しないので、新しく生まれた光子による「加熱」は期待できない。する
とニュートリノの「温度」は光子の温度より下がってしまうのである。
よりも大きいため、電子は依
然として光速に近い速さで運動しているが、その後、宇宙の温度が下がっていく
と、やがて電子の速度が光速よりも遅くなり、電子と陽電子が衝突して対消滅し、光子
ができる反応によって、ほとんどの電子と陽電子が消えてしまう。この対消滅に
伴って新しく生まれる光子による「加熱」のため、熱平衡状態にあるプラズマ粒子の
温度の低下は幾分か抑えられる。一方、ニュートリノはもはや電子や光子と
相互作用しないので、新しく生まれた光子による「加熱」は期待できない。する
とニュートリノの「温度」は光子の温度より下がってしまうのである。
![]() は光子の温度
は光子の温度![]() を用いて
を用いて
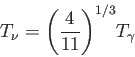
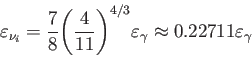
![]() を輻射質量等価時と呼ぶ。
を輻射質量等価時と呼ぶ。![]() におけるスケール因子は
におけるスケール因子は
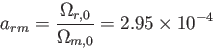
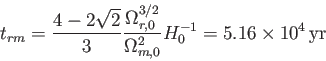
![]() に関する3次方程式を解くこと
により、スケール因子
に関する3次方程式を解くこと
により、スケール因子![]() が宇宙時間
が宇宙時間![]() の関数として求まる。しかし、やや複雑な表式になるので、
ここでは輻射優勢時(
の関数として求まる。しかし、やや複雑な表式になるので、
ここでは輻射優勢時(![]() )と質量優勢時(
)と質量優勢時(![]() )の二つの時代に分けて宇宙膨張
を考えよう。
)の二つの時代に分けて宇宙膨張
を考えよう。
![]() とおくと、
とおくと、
![]() より、
より、