次に曲率と物質と宇宙定数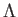 を含む3成分FRWモデルを考えよう。
宇宙の空間的な曲率は、近年の観測からほぼ平坦であると考えられているが、
パーセント以下の精度で測ると、わずかにずれている可能性も残されている。
その場合、宇宙はどのような運命をたどるのあろうか?
式(5.17)から、
を含む3成分FRWモデルを考えよう。
宇宙の空間的な曲率は、近年の観測からほぼ平坦であると考えられているが、
パーセント以下の精度で測ると、わずかにずれている可能性も残されている。
その場合、宇宙はどのような運命をたどるのあろうか?
式(5.17)から、
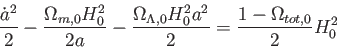 |
(5.37) |
が得られる。物質+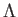 モデルと同様、重力ポテンシャルを表すのは
モデルと同様、重力ポテンシャルを表すのは
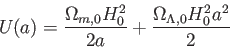 |
(5.38) |
である。しかし、曲率がある場合、式(5.37)の右辺、
すなわち力学的エネルギー
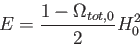 |
(5.39) |
がゼロでないので、一般にスケール因子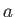 の時間発展は異なるものとなる。
の時間発展は異なるものとなる。
まず
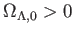 の場合を考えよう。このとき
の場合を考えよう。このとき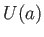 は、物質+
は、物質+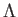 モデルと同様、
モデルと同様、
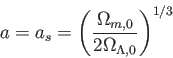 |
(5.40) |
で極大値
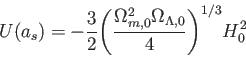 |
(5.41) |
をとる。しかし、力学的エネルギー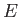 が
が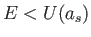 かつ
かつ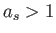 の場合、
ポテンシャル
の場合、
ポテンシャル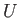 の壁を乗り越えることができない。言い換えると、
宇宙の空間成分が正に曲がりすぎていると、物質間の引力が強すぎて宇宙は永遠に膨張す
ることができず、いずれ収縮し、ビッグクランチを迎えてしまうのである。
また、
の壁を乗り越えることができない。言い換えると、
宇宙の空間成分が正に曲がりすぎていると、物質間の引力が強すぎて宇宙は永遠に膨張す
ることができず、いずれ収縮し、ビッグクランチを迎えてしまうのである。
また、
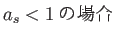 、ポテンシャルの向こう側
、ポテンシャルの向こう側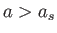 から極値に向かってやってきて、ポテン
シャルを乗り越えることができず、向こう側に戻ってしまう解も存在する。
いいかえると、宇宙は初め収縮しているのであるが、ある大きさ
から極値に向かってやってきて、ポテン
シャルを乗り越えることができず、向こう側に戻ってしまう解も存在する。
いいかえると、宇宙は初め収縮しているのであるが、ある大きさ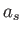 になると
収縮を止め、再び膨張し始める。これをビッグバウンスともいう。
宇宙定数による斥力によって、宇宙はゴムボールのように「弾んで」しまうので
ある。
になると
収縮を止め、再び膨張し始める。これをビッグバウンスともいう。
宇宙定数による斥力によって、宇宙はゴムボールのように「弾んで」しまうので
ある。
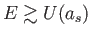 はどうであろうか?この場合、宇宙は減速膨張の後、
ポテンシャルの極値をとる
はどうであろうか?この場合、宇宙は減速膨張の後、
ポテンシャルの極値をとる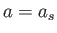 あたりでその動きをほとんど止めてしまうであろう。宇宙は長い
間、「ほぼ静止」し、その後、加速膨張へ移行する。そのような宇宙を停留宇宙とよぶ。
あたりでその動きをほとんど止めてしまうであろう。宇宙は長い
間、「ほぼ静止」し、その後、加速膨張へ移行する。そのような宇宙を停留宇宙とよぶ。
次に
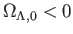 の場合を考えよう。このとき、ポテンシャル
の場合を考えよう。このとき、ポテンシャル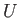 は
は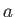 と
共に単調増加するので、
と
共に単調増加するので、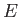 の値によらずポテンシャル
の値によらずポテンシャル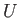 の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまり宇宙
はいずれビッグクランチを迎える。
の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまり宇宙
はいずれビッグクランチを迎える。
![]() の場合を考えよう。このとき
の場合を考えよう。このとき![]() は、物質+
は、物質+![]() モデルと同様、
モデルと同様、
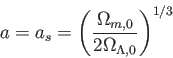
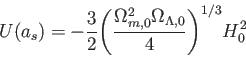
![]() の場合を考えよう。このとき、ポテンシャル
の場合を考えよう。このとき、ポテンシャル![]() は
は![]() と
共に単調増加するので、
と
共に単調増加するので、![]() の値によらずポテンシャル
の値によらずポテンシャル![]() の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまり宇宙
はいずれビッグクランチを迎える。
の壁を乗り越えることができない。
つまり、宇宙はある時刻に静止し、その後収縮してつぶれてしまう。つまり宇宙
はいずれビッグクランチを迎える。